
【题目】已知等差数列{an}的前n(n∈N*)项和为Sn , a3=3,且λSn=anan+1 , 在等比数列{bn}中,b1=2λ,b3=a15+1. (Ⅰ)求数列{an}及{bn}的通项公式;
(Ⅱ)设数列{cn}的前n(n∈N*)项和为Tn , 且 ![]() ,求Tn .
,求Tn .
【答案】解:(Ⅰ)∵λSn=anan+1 , a3=3,∴λa1=a1a2 , 且λ(a1+a2)=a2a3 , ∴a2=λ,a1+a2=a3=3,①
∵数列{an}是等差数列,∴a1+a3=2a2 , 即2a2﹣a1=3,②
由①②得a1=1,a2=2,∴an=n,λ=2,
∴b1=4,b3=16,∴{bn}的公比q= ![]() =±2,
=±2,
∴ ![]() 或bn=(﹣2)n+1 .
或bn=(﹣2)n+1 .
(Ⅱ)由(I)知 ![]() ,∴
,∴ ![]() =
= ![]() ,
,
∴Tn= ![]()
=1+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]()
= ![]() .
.
【解析】(I)分别令n=1,2列方程,再根据等差数列的性质即可求出a1 , a2得出an , 计算b1 , b3得出公比得出bn;(II)求出cn , 根据裂项法计算Tn .


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:
【题目】边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2 ![]()

(1)如图1,将△DEC沿射线方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由.
(2)如图2,将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD′、BE′.边D′E′的中点为P.
①在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由;
②连接AP,当AP最大时,求AD′的值.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,在 ![]() 中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
(1)求证: ![]() 是等腰三角形。
是等腰三角形。
(2)如图2,若将上图中的两个全等的矩形改为两个全等的正三角形( ![]() 和
和 ![]() ),其他条件不变。请探究
),其他条件不变。请探究 ![]() 的形状,并说明理由。
的形状,并说明理由。
(3)若将上图中的两个全等的矩形改为两个正方形,并把 ![]() 中的边BC缩短到如图3形状,请探究
中的边BC缩短到如图3形状,请探究 ![]() 的形状,并说明理由。
的形状,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数列{an}满足a1=3,an+1= ![]() .
.
(1)证明:数列 ![]() 是等差数列,并求{an}的通项公式;
是等差数列,并求{an}的通项公式;
(2)令bn=a1a2…an , 求数列 ![]() 的前n项和Sn .
的前n项和Sn .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( ) 
A.4.5
B.6
C.7.5
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C的参数方程为 ![]() (t为参数,a>0)以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,已知直线l的极坐标方程为
(t为参数,a>0)以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,已知直线l的极坐标方程为 ![]() . (Ⅰ)设P是曲线C上的一个动点,当a=2时,求点P到直线l的距离的最小值;
. (Ⅰ)设P是曲线C上的一个动点,当a=2时,求点P到直线l的距离的最小值;
(Ⅱ)若曲线C上的所有点均在直线l的右下方,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知椭圆Γ: ![]() 经过点
经过点 ![]() ,且离心率为
,且离心率为 ![]() .
.
(1)求椭圆Γ的方程;
(2)直线l与圆O:x2+y2=b2相切于点M,且与椭圆Γ相交于不同的两点A,B,求|AB|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四个函数:①y=xsinx;②y=xcosx;③y=x|cosx|;④y=x2x的图象(部分)如图: 
则按照从左到右图象对应的函数序号安排正确的一组是( )
A.①④③②
B.③④②①
C.④①②③
D.①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为 ![]() 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( ) 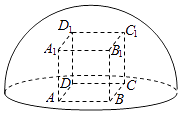
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com