Question

【题目】在直角坐标系xoy中，曲线C的参数方程为 （t为参数，a＞0）以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系，已知直线l的极坐标方程为 ． （Ⅰ）设P是曲线C上的一个动点，当a=2时，求点P到直线l的距离的最小值；
（Ⅱ）若曲线C上的所有点均在直线l的右下方，求a的取值范围．

Answer 1

【答案】解：（Ⅰ）由 ，得 ， 化成直角坐标方程，得 ，即直线l的方程为x﹣y+4=0．
依题意，设P（2cost，2sint），则P到直线l的距离 ，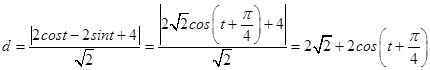
当 ，即 时， ．
故点P到直线l的距离的最小值为 ．
（Ⅱ）∵曲线C上的所有点均在直线l的右下方，∴对t∈R，有acost﹣2sint+4＞0恒成立，
即 （其中 ）恒成立，∴ ，又a＞0，解得 ，
故a的取值范围为
【解析】（Ⅰ）求出直线的普通方程，设P（2cost，2sint），则P到直线l的距离 ，即可求点P到直线l的距离的最小值；（Ⅱ）若曲线C上的所有点均在直线l的右下方，则对t∈R，有acost﹣2sint+4＞0恒成立，即 （其中 ）恒成立，即可求a的取值范围．