
【题目】已知点F2 , P分别为双曲线 ![]() 的右焦点与右支上的一点,O为坐标原点,若2
的右焦点与右支上的一点,O为坐标原点,若2 ![]() |,且
|,且 ![]() ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:方法一:设P(x,y),F1(﹣c,0),F2(c,0),
由题意可知:2 ![]() =
= ![]() +
+ ![]() ,则M为线段PF2的中点,则M(
,则M为线段PF2的中点,则M( ![]() ,
, ![]() ),
),
则 ![]() =(c,0),
=(c,0), ![]() =(
=( ![]() ,
, ![]() ),
),
则 ![]()
![]() =
= ![]() ×c=
×c= ![]() 解得:x=2c,
解得:x=2c,
由丨 ![]() 丨=丨
丨=丨 ![]() 丨=c,即
丨=c,即 ![]() =c,解得:y=
=c,解得:y= ![]() c,
c,
则P(2c, ![]() c),由双曲线的定义可知:丨PF1丨﹣丨PF2丨=2a,
c),由双曲线的定义可知:丨PF1丨﹣丨PF2丨=2a,
即 ![]() ﹣
﹣ ![]() =2a,a=(
=2a,a=( ![]() ﹣1)c,
﹣1)c,
由双曲线的离心率e= ![]() =
= ![]() ,
,
∴该双曲线的离心率 ![]() ,
,
故选D. 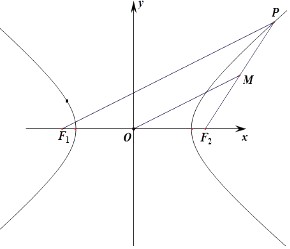
方法二:由题意可知:2 ![]() =
= ![]() +
+ ![]() ,则M为线段PF2的中点,
,则M为线段PF2的中点,
则OM为△F2F1P的中位线,![]()
![]() =﹣
=﹣ ![]()
![]() =﹣丨
=﹣丨 ![]() 丨丨
丨丨 ![]() 丨cos∠OF2M=
丨cos∠OF2M= ![]() ,
,
由丨 ![]() 丨=丨
丨=丨 ![]() 丨=c,则cos∠OF2M=﹣
丨=c,则cos∠OF2M=﹣ ![]() ,
,
由正弦定理可知:丨OM丨2=丨 ![]() 丨2+丨
丨2+丨 ![]() 丨2﹣2丨
丨2﹣2丨 ![]() 丨丨
丨丨 ![]() 丨cos∠OF2M=3c2 ,
丨cos∠OF2M=3c2 ,
则丨OM丨= ![]() c,则丨PF1丨=2
c,则丨PF1丨=2 ![]() ,丨PF2丨=丨MF2丨=2c,
,丨PF2丨=丨MF2丨=2c,
由双曲线的定义丨PF1丨﹣丨PF2丨=2a,a=( ![]() ﹣1)c,
﹣1)c,
由双曲线的离心率e= ![]() =
= ![]() ,
,
∴该双曲线的离心率 ![]() ,
,
故选D.
方法一:由题意可知:则M为线段PF2的中点,则M( ![]() ,
, ![]() ),根据向量数量积的坐标运算,即可求得x=2c,利用两点之间的距离公式,即可求得y=
),根据向量数量积的坐标运算,即可求得x=2c,利用两点之间的距离公式,即可求得y= ![]() c,利用双曲线的定义,即可求得a=(
c,利用双曲线的定义,即可求得a=( ![]() ﹣1)c,利用双曲线的离心率公式即可求得该双曲线的离心率.
﹣1)c,利用双曲线的离心率公式即可求得该双曲线的离心率.
方法二:由题意可知:2 ![]() =
= ![]() +
+ ![]() ,则M为线段PF2的中点,根据向量的数量积,求得cos∠OF2M,利用余弦定理即可求得丨OM丨,根据三角形的中位线定理及双曲线的定义丨PF1丨﹣丨PF2丨=2a,a=(
,则M为线段PF2的中点,根据向量的数量积,求得cos∠OF2M,利用余弦定理即可求得丨OM丨,根据三角形的中位线定理及双曲线的定义丨PF1丨﹣丨PF2丨=2a,a=( ![]() ﹣1)c,即可求得双曲线的离心率.
﹣1)c,即可求得双曲线的离心率.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】贵州省是我国首个大数据综合试验区,大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值,为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题: 
(1)本次参与调查的人数有人;
(2)关注城市医疗信息的有人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是度;
(4)说一条你从统计图中获取的信息.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数列{an}满足a1=3,an+1= ![]() .
.
(1)证明:数列 ![]() 是等差数列,并求{an}的通项公式;
是等差数列,并求{an}的通项公式;
(2)令bn=a1a2…an , 求数列 ![]() 的前n项和Sn .
的前n项和Sn .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xoy中,曲线C的参数方程为 ![]() (t为参数,a>0)以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,已知直线l的极坐标方程为
(t为参数,a>0)以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,已知直线l的极坐标方程为 ![]() . (Ⅰ)设P是曲线C上的一个动点,当a=2时,求点P到直线l的距离的最小值;
. (Ⅰ)设P是曲线C上的一个动点,当a=2时,求点P到直线l的距离的最小值;
(Ⅱ)若曲线C上的所有点均在直线l的右下方,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知椭圆Γ: ![]() 经过点
经过点 ![]() ,且离心率为
,且离心率为 ![]() .
.
(1)求椭圆Γ的方程;
(2)直线l与圆O:x2+y2=b2相切于点M,且与椭圆Γ相交于不同的两点A,B,求|AB|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地的铁路路程约为615千米,高铁速度为300千米/小时,直达;动车速度为200千米/小时,行驶180千米后,中途要停靠徐州10分钟,若动车先出发半小时,两车与甲地之间的距离y(千米)与动车行驶时间x(小时)之间的函数图象为( )
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四个函数:①y=xsinx;②y=xcosx;③y=x|cosx|;④y=x2x的图象(部分)如图: 
则按照从左到右图象对应的函数序号安排正确的一组是( )
A.①④③②
B.③④②①
C.④①②③
D.①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题获得学分2分,便可通过考察.已知6道备选题中考生甲有4题能正确完成:考生乙每题正确完成的概率都是 ![]() ,且每题正确完成与否互不影响.求: (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
,且每题正确完成与否互不影响.求: (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(Ⅱ)请你判断两考生的实验操作学科能力,比较他们能通过本次考查的可能性大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 ![]() . (Ⅰ)求函数f(x)的单调递增区间;
. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,内角A、B、C的对边分别为a、b、c.已知 ![]() ,a=2,
,a=2, ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com