练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，直四棱柱ABCD﹣A1B1C1D1内接于半径为 的半球O，四边形ABCD为正方形，则该四棱柱的体积最大时，AB的长是（ ）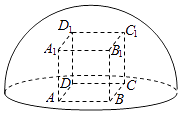
    A.1
    B.
    C.
    D.2

    【答案】D
    【解析】解：设AB=a，BB1=h， 则OB= a，连接OB1 ， OB，则OB2+BB12=OB12=3，
    ∴ =3，
    ∴a2=6﹣2h2 ，
    故正四棱柱的体积是V=a2h=6h﹣2h3 ，
    ∴V′=6﹣6h2 ，
    当0＜h＜1时，V′＞0，1＜h＜ 时，V′＜0，
    ∴h=1时，该四棱柱的体积最大，此时AB=2．
    故选：D．

    设AB=a，BB1=h，求出a2=6﹣2h2 ， 故正四棱柱的体积是V=a2h=6h﹣2h3 ， 利用导数，得到该正四棱柱体积的最大值，即可得出结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知等差数列{an}的前n（n∈N*）项和为Sn ， a3=3，且λSn=anan+1 ， 在等比数列{bn}中，b1=2λ，b3=a15+1． （Ⅰ）求数列{an}及{bn}的通项公式；
    （Ⅱ）设数列{cn}的前n（n∈N*）项和为Tn ， 且 ，求Tn ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数f（x）=（x2﹣2x）1nx+ax2+2，g（x）=f（x）﹣x﹣2． （Ⅰ）当a=﹣1时，求f（x）在（1，f（1））处的切线方程；
    （Ⅱ）若a＞0且函数g（x）有且仅有一个零点，求实数a的值；
    （Ⅲ）在（Ⅱ）的条件下，若e﹣2＜x＜e时，g（x）≤m恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知集合A={x∈N|x＜3}，B={x|x=a﹣b，a∈A，b∈A}，则A∩B=（ ）
    A.{1，2}
    B.{﹣2，﹣1，0，1，2}
    C.{1}
    D.{0，1，2}

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数f（x）= ．
    （1）证明：k∈R，直线y=g（x）都不是曲线y=f（x）的切线；
    （2）若x∈[e，e2]，使得f（x）≤g（x）+ 成立，求实数k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD= AD，E为AD的中点，异面直线AP与CD所成的角为90°．
    （Ⅰ）证明：△PBE是直角三角形；
    （Ⅱ）若二面角P﹣CD﹣A的大小为45°，求二面角A﹣PE﹣C的余弦值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设函数f（x）= ，则满足f（f（m））=3f（m）的实数m的取值范围是（ ）
    A.（﹣∞，0）∪{﹣ }
    B.[0，1]
    C.[0，+∞）∪{﹣ }
    D.[1，+∞）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知数列{an} 满足a1= ，a2= ，an+2﹣an+1=（﹣1）n+1（an+1﹣an）（n∈N*），数列{an}的前n项和为Sn ， 则S2017= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，线段AB经过平移得到线段A′B′，其中点A，B的对应点分别为点A′，B′，这四个点都在格点上，则这四个点组成的四边形ABB′A′的面积是（ ）

    A.4
    B.6
    C.9
    D.13

    查看答案和解析>>

    同步练习册答案