
【题目】设函数f(x)= ![]() ,则满足f(f(m))=3f(m)的实数m的取值范围是( )
,则满足f(f(m))=3f(m)的实数m的取值范围是( )
A.(﹣∞,0)∪{﹣ ![]() }
}
B.[0,1]
C.[0,+∞)∪{﹣ ![]() }
}
D.[1,+∞)
科目:初中数学 来源: 题型:
【题目】已知椭圆Γ: ![]() 经过点
经过点 ![]() ,且离心率为
,且离心率为 ![]() .
.
(1)求椭圆Γ的方程;
(2)直线l与圆O:x2+y2=b2相切于点M,且与椭圆Γ相交于不同的两点A,B,求|AB|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,E为A1C1的中点, ![]()

(Ⅰ)证明:CE⊥平面AB1C1;
(Ⅱ)若AA1= ![]() ,∠BAC=30°,求点E到平面AB1C的距离.
,∠BAC=30°,求点E到平面AB1C的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为 ![]() 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( ) 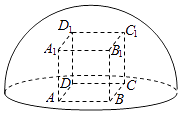
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆E:(x+ ![]() )2+y2=16,点F(
)2+y2=16,点F( ![]() ,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹E的方程; (Ⅱ)直线l过点(1,1),且与轨迹Γ交于A,B两点,点M满足
,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹E的方程; (Ⅱ)直线l过点(1,1),且与轨迹Γ交于A,B两点,点M满足 ![]() =
= ![]() ,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 ![]() . (Ⅰ)求函数f(x)的单调递增区间;
. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,内角A、B、C的对边分别为a、b、c.已知 ![]() ,a=2,
,a=2, ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有五人五钱,令上二人所得与下三人等.问各得几何?”其意思为:“现有甲乙丙丁戊五人依次差值等额分五钱,要使甲乙两人所得的钱与丙丁戊三人所得的钱相等,问每人各得多少钱?”根据题意,乙得( )
A.![]() 钱
钱
B.![]() 钱
钱
C.1钱
D.![]() 钱
钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旭日商场销售A,B两种品牌的钢琴,这两种钢琴的进价和售价如下表所示:
A | B | |
进价(万元/.套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种钢琴若干套,共需66万元,全部销售后可获毛利润9万元.(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进A,B两种品牌的钢琴各多少套?
(2)通过市场调查,该商场决定在原计划的基础上,减少A种钢琴的购进数量,增加B种钢琴的购进数量,已知B种钢琴增加的数量是A种钢琴减少数量的1.5倍,若用于购进这两种钢琴的总资金不超过69万元,问A种钢琴购进数量至多或减少多少套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com