
【题目】已知集合A={x∈N|x<3},B={x|x=a﹣b,a∈A,b∈A},则A∩B=( )
A.{1,2}
B.{﹣2,﹣1,0,1,2}
C.{1}
D.{0,1,2}
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知数列{an}满足a1=3,an+1= ![]() .
.
(1)证明:数列 ![]() 是等差数列,并求{an}的通项公式;
是等差数列,并求{an}的通项公式;
(2)令bn=a1a2…an , 求数列 ![]() 的前n项和Sn .
的前n项和Sn .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四个函数:①y=xsinx;②y=xcosx;③y=x|cosx|;④y=x2x的图象(部分)如图: 
则按照从左到右图象对应的函数序号安排正确的一组是( )
A.①④③②
B.③④②①
C.④①②③
D.①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题获得学分2分,便可通过考察.已知6道备选题中考生甲有4题能正确完成:考生乙每题正确完成的概率都是 ![]() ,且每题正确完成与否互不影响.求: (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
,且每题正确完成与否互不影响.求: (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(Ⅱ)请你判断两考生的实验操作学科能力,比较他们能通过本次考查的可能性大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,E为A1C1的中点, ![]()

(Ⅰ)证明:CE⊥平面AB1C1;
(Ⅱ)若AA1= ![]() ,∠BAC=30°,求点E到平面AB1C的距离.
,∠BAC=30°,求点E到平面AB1C的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名维修工人进行维修,每台机器出现故障需要维修的概率为 ![]() . (Ⅰ)若出现故障的机器台数为x,求x的分布列;
. (Ⅰ)若出现故障的机器台数为x,求x的分布列;
(Ⅱ)该厂至少有多少名维修工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(Ⅲ)已知一名维修工人每月只有维修1台机器的能力,每月需支付给每位维修工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名维修工人,求该厂每月获利的均值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为 ![]() 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( ) 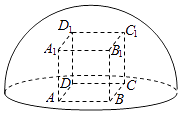
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 ![]() . (Ⅰ)求函数f(x)的单调递增区间;
. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,内角A、B、C的对边分别为a、b、c.已知 ![]() ,a=2,
,a=2, ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com