
【题目】已知函数f(x)= ![]() .
.
(1)证明:k∈R,直线y=g(x)都不是曲线y=f(x)的切线;
(2)若x∈[e,e2],使得f(x)≤g(x)+ ![]() 成立,求实数k的取值范围.
成立,求实数k的取值范围.
【答案】
(1)解:证明:f(x)的定义域为(0,1)∪(1,+∞),
f(x)的导数为f′(x)= ![]() ,
,
直线y=g(x)过定点(1,0),
若直线y=g(x)与y=f(x)相切于点(m, ![]() ),
),
则k= ![]() =
= ![]() ,即为lnm+m﹣1=0①
,即为lnm+m﹣1=0①
设h(x)=lnx+x﹣1,h′(x)= ![]() +1>0,
+1>0,
则h(x)在(0,+∞)递增,h(1)=0,当且仅当m=1①成立.
与定义域矛盾,故k∈R,直线y=g(x)都不是曲线y=f(x)的切线;
(2)解:f(x)≤g(x)+ ![]()
![]() ﹣k(x﹣1)≤
﹣k(x﹣1)≤ ![]() ,可令m(x)=
,可令m(x)= ![]() ﹣k(x﹣1),x∈[e,e2],
﹣k(x﹣1),x∈[e,e2],
则x∈[e,e2],使得f(x)≤g(x)+ ![]() 成立m(x)min≤
成立m(x)min≤ ![]() .
.
m′(x)= ![]() ﹣k=﹣(
﹣k=﹣( ![]() ﹣
﹣ ![]() )2+
)2+ ![]() ﹣k,
﹣k,
当k≥ ![]() 时,m′(x)≤0,m(x)在[e,e2]递减,于是m(x)min=m(e2)=
时,m′(x)≤0,m(x)在[e,e2]递减,于是m(x)min=m(e2)= ![]() ﹣k(e2﹣1)≤
﹣k(e2﹣1)≤ ![]() ,
,
解得k≥ ![]() ,满足k≥
,满足k≥ ![]() ,故k≥
,故k≥ ![]() 成立;
成立;
当k< ![]() 时,由y=﹣(t﹣
时,由y=﹣(t﹣ ![]() )2+
)2+ ![]()
![]() 得m′(x)=﹣(
得m′(x)=﹣( ![]() ﹣
﹣ ![]() )2+
)2+ ![]() ﹣k在[e,e2]递增,
﹣k在[e,e2]递增,
m′(e)≤m′(x)≤m′(e2),即﹣k≤m′(x)≤ ![]() ﹣k,
﹣k,
①若﹣k≥0即k≤0,m′(x)≥0,则m(x)在[e,e2]递增,m(x)min=m(e)=e﹣k(e﹣1)≥e> ![]() ,不成立;
,不成立;
②若﹣k<0,即0<k< ![]() 时,由m′(e)=﹣k<0,m′(e2)=
时,由m′(e)=﹣k<0,m′(e2)= ![]() ﹣k>0,
﹣k>0,
由m′(x)单调性可得x0∈[e,e2],由m′(x0)=0,且当x∈(e,x0),m′(x)<0,m(x)递减;
当x∈(x0,e2)时,m′(x)>0,m(x)递增,
可得m(x)的最小值为 ![]() +k(x0﹣1),由
+k(x0﹣1),由 ![]() +k(x0﹣1)≤
+k(x0﹣1)≤ ![]() ,可得k≥
,可得k≥ ![]() (
( ![]() ﹣
﹣ ![]() )
)
> ![]() (
( ![]() )=
)= ![]() >
> ![]() ,与0<k<
,与0<k< ![]() 矛盾.
矛盾.
综上可得k的范围是k≥ ![]() .
.
【解析】(1)求出f(x)的导数,可得切线的斜率,设出切点,构造函数h(x)=lnx+x﹣1,求出导数和单调区间,即可得证;(2)f(x)≤g(x)+ ![]()
![]() ﹣k(x﹣1)≤
﹣k(x﹣1)≤ ![]() ,可令m(x)=
,可令m(x)= ![]() ﹣k(x﹣1),x∈[e,e2],则x∈[e,e2],使得f(x)≤g(x)+
﹣k(x﹣1),x∈[e,e2],则x∈[e,e2],使得f(x)≤g(x)+ ![]() 成立m(x)min≤
成立m(x)min≤ ![]() .对k讨论,当k≥
.对k讨论,当k≥ ![]() 时,当k<
时,当k< ![]() 时,运用单调性,求出最小值,解不等式即可得到所求范围.
时,运用单调性,求出最小值,解不等式即可得到所求范围.


科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( ) 
A.4.5
B.6
C.7.5
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,E为A1C1的中点, ![]()

(Ⅰ)证明:CE⊥平面AB1C1;
(Ⅱ)若AA1= ![]() ,∠BAC=30°,求点E到平面AB1C的距离.
,∠BAC=30°,求点E到平面AB1C的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.
(1)若点A1的坐标为(2,1),则点A4的坐标为_____;
(2)若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为 ![]() 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( ) 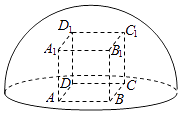
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆E:(x+ ![]() )2+y2=16,点F(
)2+y2=16,点F( ![]() ,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹E的方程; (Ⅱ)直线l过点(1,1),且与轨迹Γ交于A,B两点,点M满足
,0),P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(Ⅰ)求动点Q的轨迹E的方程; (Ⅱ)直线l过点(1,1),且与轨迹Γ交于A,B两点,点M满足 ![]() =
= ![]() ,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
,点O为坐标原点,延长线段OM与轨迹Γ交于点R,四边形OARB能否为平行四边形?若能,求出此时直线l的方程,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有五人五钱,令上二人所得与下三人等.问各得几何?”其意思为:“现有甲乙丙丁戊五人依次差值等额分五钱,要使甲乙两人所得的钱与丙丁戊三人所得的钱相等,问每人各得多少钱?”根据题意,乙得( )
A.![]() 钱
钱
B.![]() 钱
钱
C.1钱
D.![]() 钱
钱
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com