
【题目】已知函数f(x)=(x2﹣2x)1nx+ax2+2,g(x)=f(x)﹣x﹣2. (Ⅰ)当a=﹣1时,求f(x)在(1,f(1))处的切线方程;
(Ⅱ)若a>0且函数g(x)有且仅有一个零点,求实数a的值;
(Ⅲ)在(Ⅱ)的条件下,若e﹣2<x<e时,g(x)≤m恒成立,求实数m的取值范围.
【答案】解:(Ⅰ)当a=﹣1时,f(x)=(x2﹣2x)1nx﹣x2+2定义域(0,+∞), f'(x)=(2x﹣2)1nx+(x﹣2)﹣2x,
∴f'(1)=﹣3,又f(1)=1,
∴f(x)在(1,f(1))处的切线方程3x+y﹣4=0.
(Ⅱ)令g(x)=f(x)﹣x﹣2=0,则(x2﹣2x)1nx+ax2+2=x+2
即 ![]()
令 ![]() ,
,
则 ![]() =
= ![]() ,
,
令t(x)=1﹣x﹣21nx,则 ![]() ,
,
∵x∈(0,+∞),∴t'(x)<0,
∴t(x)在(0,+∞)上是减函数,
又∵t(1)=h'(1)=0,
∴当0<x<1时,h'(x)>0,当x>1时,h'(x)<0,
∴h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴h(x)max=h(1)=1>0,
又∵ ![]() ,
, ![]() ,a>0
,a>0
∴当函数g(x)有且仅有一个零点时,a=1
(Ⅲ)当a=1,g(x)=(x2﹣2x)1nx+x2﹣x,若e﹣2<x<e,g(x)≤m,
只需证明g(x)max≤m,g'(x)=(x﹣1)(3+21nx)
令g'(x)=0得x=1或 ![]() ,又∵e﹣2<x<e,
,又∵e﹣2<x<e,
∴函数g(x)在 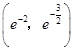 上单调递增,
上单调递增,
在 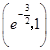 上单调递减,在(1,e)上单调递增,
上单调递减,在(1,e)上单调递增,
即 ![]() 是g(x)的极大值点,
是g(x)的极大值点,
又  ,g(e)=2e2﹣3e
,g(e)=2e2﹣3e
∵ 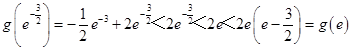 ,
,
∴ 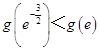 ,∴m≥2e2﹣3e,
,∴m≥2e2﹣3e,
∴实数m的取值范围是(2e2﹣3e,+∞).
【解析】(Ⅰ)当a=﹣1时,f'(x)=(2x﹣2)1nx+(x﹣2)﹣2x,由此利用导数的几何意义能求出f(x)在(1,f(1))处的切线方程.(Ⅱ)令g(x)=f(x)﹣x﹣2=0,则 ![]() 令
令 ![]() ,则h′(x)=
,则h′(x)= ![]() ,令t(x)=1﹣x﹣21nx,则
,令t(x)=1﹣x﹣21nx,则 ![]() ,由此利用导数性质能求出当函数g(x)有且仅有一个零点时a的值.(Ⅲ)当a=1,若e﹣2<x<e,g(x)≤m,只需证明g(x)max≤m,由g'(x)=(x﹣1)(3+21nx),求出
,由此利用导数性质能求出当函数g(x)有且仅有一个零点时a的值.(Ⅲ)当a=1,若e﹣2<x<e,g(x)≤m,只需证明g(x)max≤m,由g'(x)=(x﹣1)(3+21nx),求出 ![]() 是g(x)的极大值点,由此能求出实数m的取值范围.
是g(x)的极大值点,由此能求出实数m的取值范围.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的最大(小)值与导数(求函数
在这个区间单调递减),还要掌握函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.
比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知,如图1,在 ![]() 中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
中,AC=BC,点D是边AB的中点,E,F分别是AC和BC的中点,分别以CE,CF为一边向上作两个全等的矩形CEGH和矩形CFMN(其中EG=FM),依次连结DG、DM、GM。
(1)求证: ![]() 是等腰三角形。
是等腰三角形。
(2)如图2,若将上图中的两个全等的矩形改为两个全等的正三角形( ![]() 和
和 ![]() ),其他条件不变。请探究
),其他条件不变。请探究 ![]() 的形状,并说明理由。
的形状,并说明理由。
(3)若将上图中的两个全等的矩形改为两个正方形,并把 ![]() 中的边BC缩短到如图3形状,请探究
中的边BC缩短到如图3形状,请探究 ![]() 的形状,并说明理由。
的形状,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知椭圆Γ: ![]() 经过点
经过点 ![]() ,且离心率为
,且离心率为 ![]() .
.
(1)求椭圆Γ的方程;
(2)直线l与圆O:x2+y2=b2相切于点M,且与椭圆Γ相交于不同的两点A,B,求|AB|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四个函数:①y=xsinx;②y=xcosx;③y=x|cosx|;④y=x2x的图象(部分)如图: 
则按照从左到右图象对应的函数序号安排正确的一组是( )
A.①④③②
B.③④②①
C.④①②③
D.①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中2题获得学分2分,便可通过考察.已知6道备选题中考生甲有4题能正确完成:考生乙每题正确完成的概率都是 ![]() ,且每题正确完成与否互不影响.求: (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
,且每题正确完成与否互不影响.求: (Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(Ⅱ)请你判断两考生的实验操作学科能力,比较他们能通过本次考查的可能性大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,E为A1C1的中点, ![]()

(Ⅰ)证明:CE⊥平面AB1C1;
(Ⅱ)若AA1= ![]() ,∠BAC=30°,求点E到平面AB1C的距离.
,∠BAC=30°,求点E到平面AB1C的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直四棱柱ABCD﹣A1B1C1D1内接于半径为 ![]() 的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( )
的半球O,四边形ABCD为正方形,则该四棱柱的体积最大时,AB的长是( ) 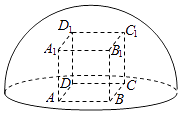
A.1
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com