
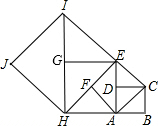
 如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第2015个正方形的面积S2015为22014.
如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第2015个正方形的面积S2015为22014. 分析 由题意可以知道第一个正方形的边长为1,第二个正方形的边长为$\sqrt{2}$,第三个正方形的边长为2,就有第n个正方形的边长为$\sqrt{2}$(n-1),再根据正方形的面积公式就可以求出结论.
解答 解:第一个正方形的面积为1=,故其边长为1=20;
第二个正方形的边长为$\sqrt{2}$,其面积为2=21;
第三个正方形的边长为2,其面积为4=22;
第四个正方形的边长为2$\sqrt{2}$,其面积为8=23;
…
第n个正方形的边长为($\sqrt{2}$)n-1,其面积为2n-1.
当n=2015时,
S2015=22015-1=22014.
故答案为:22014.
点评 本题考查了正方形的面积公式的运用以及正方形的性质及勾股定理得运用,是一道探索规律的试题,解答本题时找到正方形的面积与边长的变化规律是关健.


科目:初中数学 来源: 题型:选择题
 如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为3,则等边三角形ABC的边长为( )
如图,⊙O是等边三角形ABC的外接圆,⊙O的半径为3,则等边三角形ABC的边长为( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{9}{8}$ | B. | m≥$\frac{9}{8}$ | C. | m≤$\frac{9}{8}$ | D. | m<$\frac{9}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
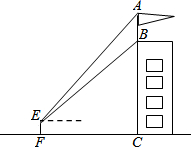 如图,某建筑物BC上有一旗杆AB,小刘在与BC相距24m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°,小刘的观测点与地面的距离EF为1.6m.
如图,某建筑物BC上有一旗杆AB,小刘在与BC相距24m的F处,由E点观测到旗杆顶部A的仰角为52°、底部B的仰角为45°,小刘的观测点与地面的距离EF为1.6m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大为原来的8倍 | ||
| C. | 缩小为原来的$\frac{1}{8}$ | D. | 扩大为原来的16倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
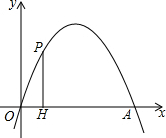 如图,抛物线y=-x2+mx过点A(4,0),O位坐标原点,设点P是x轴上方抛物线上的一个动点,过点P作PH⊥x轴,H为垂足,则PH+HO最大值为$\frac{25}{4}$.
如图,抛物线y=-x2+mx过点A(4,0),O位坐标原点,设点P是x轴上方抛物线上的一个动点,过点P作PH⊥x轴,H为垂足,则PH+HO最大值为$\frac{25}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com