

分析 (1)设本次被调查的学生数为x人,由题意x•10%=10,解得x=100,求出C组的圆心角即可解决问题.
(2)求出A、B两组的人数,即可解决问题.
(3)利用样本估计总体的思想解决问题即可.
解答 解:(1)设本次被调查的学生数为x人,
由题意x•10%=10,解得x=100,
C部分所占扇形的圆心角为360×10%=36°,
∴A部分所占扇形的圆心角为360°-36°-72°=252°,
故答案为252°,100.
(2)由题意A组人数为100×$\frac{252}{360}$=70人,B组人数为100-72-10=18人,
条形图如图所示,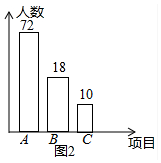
(3)样本中满意的学生占90%,
∴全校有500名就餐学生,估计该校对“午餐服务工程”表示满意的学生数为500×90%=450人.
点评 本题考查条形统计图、扇形统计图、样本估计总体的思想等知识,解题的关键是读懂图象信息,用方程的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
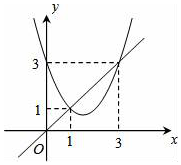 函数y=x2+bx+c与y=x的图象如图所示,有以下结论①b2-4c≥0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0.其中正确的个数为( )
函数y=x2+bx+c与y=x的图象如图所示,有以下结论①b2-4c≥0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b-1)x+c<0.其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
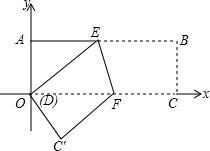 如图,在直角坐标系中,长方形纸片ABCD的边AB∥CO,点B坐标为(9,3),若把图形按如图所示折叠,使B、D两点重合,折痕为EF.
如图,在直角坐标系中,长方形纸片ABCD的边AB∥CO,点B坐标为(9,3),若把图形按如图所示折叠,使B、D两点重合,折痕为EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com