
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,
, ![]() ,
, ![]() ,
,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ,③
,③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() .其中正确的为___________.
.其中正确的为___________.
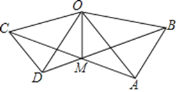
【答案】①②④
【解析】
由SAS证明△AOC≌△BOD得出∠OCA=∠ODB,AC=BD,①正确;由全等三角形的性质得出∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,得出∠AMB=∠AOB=40°,②正确;作OG⊥MC于G,OH⊥MB于H,如图所示:则∠OGC=∠OHD=90°,由AAS证明△OCG≌△ODH(AAS),得出OG=OH,由角平分线的判定方法得出MO平分∠BMC,④正确;由∠AOB=∠COD,得出当∠DOM=∠AOM时,OM才平分∠BOC,假设∠DOM=∠AOM,由△AOC≌△BOD得出∠COM=∠BOM,由MO平分∠BMC得出∠CMO=∠BMO,推出△COM≌△BOM,得OB=OC,而OA=OB,所以OA=OC,而OA>OC,故③错误;即可得出结论.
∵∠AOB=∠COD=40°,
∴∠AOB+∠AOD=∠COD+∠AOD,
即∠AOC=∠BOD,
在△AOC和△BOD中,
 ,
,
∴△AOC≌△BOD(SAS),
∴∠OCA=∠ODB,AC=BD,①正确;
∴∠OAC=∠OBD,
由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,
∴∠AMB=∠AOB=40°,②正确;
作OG⊥MC于G,OH⊥MB于H,如图2所示:
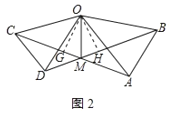
则∠OGC=∠OHD=90°,
在△OCG和△ODH中,
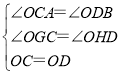 ,
,
∴△OCG≌△ODH(AAS),
∴OG=OH,
∴MO平分∠BMC,④正确;
∵∠AOB=∠COD,
∴当∠DOM=∠AOM时,OM才平分∠BOC,
假设∠DOM=∠AOM
∵△AOC≌△BOD,
∴∠COM=∠BOM,
∵MO平分∠BMC,
∴∠CMO=∠BMO,
在△COM和△BOM中,
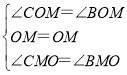 ,
,
∴△COM≌△BOM(ASA),
∴OB=OC,
∵OA=OB
∴OA=OC
与OA>OC矛盾,
∴③错误;
故答案为:①②④.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
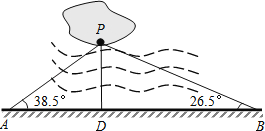
【题目】如图,益阳市梓山湖中有一孤立小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,小张在小道上测得如下数据:AB=80.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小张求出小桥PD的长并确定小桥在小道上的位置.(以A,B为参照点,结果精确到0.1米)
(参考数据:sin38.5°=0.62,cos38.5°=0.78,tan38.5°=0.80,sin26.5°=0.45,cos26.5°=0.89,tan26.5°=0.50)
查看答案和解析>>
科目:初中数学 来源: 题型:
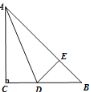
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.已知CD=2,则AB的长度等于____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
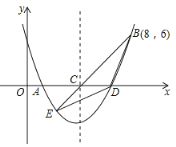
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及D点的坐标;
(3)该二次函数的对称轴交x轴于C点,连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
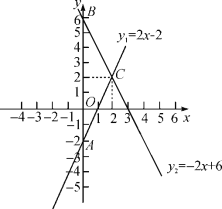
【题目】如图,直线y1=2x-2的图像与y轴交于点A,直线y2=-2x+6的图像与y轴交于点B,两者相交于点C.
(1)方程组![]() 的解是______;
的解是______;
(2)当y1>0与y2>0同时成立时,x的取值范围为_____;
(3)求△ABC的面积;
(4)在直线y1=2x-2的图像上存在异于点C的另一点P,使得△ABC与△ABP的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与![]() 轴交于点
轴交于点![]() ,
,![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() ,
,![]() 是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点
是二次函数图象上关于抛物线对称轴的一对对称点,一次函数的图象过点![]() ,
,![]() .
.
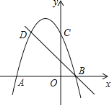
![]() 请直接写出点
请直接写出点![]() 的坐标;
的坐标;
![]() 求二次函数的解析式;
求二次函数的解析式;
![]() 根据图象直接写出一次函数值大于二次函数值的
根据图象直接写出一次函数值大于二次函数值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,反比例函数y=![]() (x>0)的图象经过点A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连接AD,DC,CB.
(x>0)的图象经过点A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,AC与BD交于点E,连接AD,DC,CB.
(1)求k的值;
(2)求证:DC∥AB;
(3)当AD∥BC时,求直线AB的函数表达式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com