
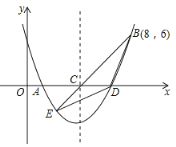
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及D点的坐标;
(3)该二次函数的对称轴交x轴于C点,连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
【答案】(1)y=![]() x2﹣4x+6;(2)函数图象的顶点坐标为(4,-2),点D的坐标为(6,0);(3)
x2﹣4x+6;(2)函数图象的顶点坐标为(4,-2),点D的坐标为(6,0);(3)![]() .
.
【解析】
(1)∵二次函数y=![]() x2+bx+c的图象过A(2,0),B(8,6)
x2+bx+c的图象过A(2,0),B(8,6)
∴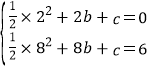 ,解得
,解得![]()
∴二次函数解析式为:y=![]() x2-4x+6,
x2-4x+6,
(2)由y=![]() x2-4x+6,得y=
x2-4x+6,得y=![]() (x-4)2-2,
(x-4)2-2,
∴函数图象的顶点坐标为(4,-2),
∵点A,D是y=![]() x2+bx+c与x轴的两个交点,
x2+bx+c与x轴的两个交点,
又∵点A(2,0),对称轴为x=4,
∴点D的坐标为(6,0).
(3)∵二次函数的对称轴交x轴于C点.
∴C点的坐标为(4,0)
∵B(8,6),
设BC所在的直线解析式为y=kx+b′,
∴![]() ,
,
解得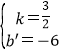 ,
,
∴BC所在的直线解析式为y=![]() x-6,
x-6,
∵E点是y=![]() x-6与y=
x-6与y=![]() x2-4x+6的交点,
x2-4x+6的交点,
∴![]() x-6=
x-6=![]() x2-4x+6
x2-4x+6
解得x1=3,x2=8(舍去),
当x=3时,y=-![]() ,
,
∴E(3,-![]() ),
),
∴△BDE的面积=△CDB的面积+△CDE的面积=![]() ×2×6+
×2×6+![]() ×2×
×2×![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一个装有进水管出水管的容器,从某时刻起只打开进水管进水,经过一段时间,在打开出水管放水,至15分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(升)与时间x(分钟)之间的关系如图所示,关停进水管后,经过_____________分钟,容器中的水恰好放完.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() 与x轴,y轴分别交于A,B两点,在y轴上有一点
与x轴,y轴分别交于A,B两点,在y轴上有一点![]() ,动点M从点A以每秒1个单位的速度沿x轴向左移动.
,动点M从点A以每秒1个单位的速度沿x轴向左移动.

(1)求A,B两点的坐标;
(2)求![]() 的面积S与动点M的移动时间t(秒)之间的函数关系式;
的面积S与动点M的移动时间t(秒)之间的函数关系式;
(3)当t为何值时![]() ?并求此时点M的坐标.
?并求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何模型:
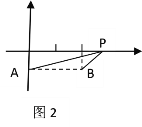
条件:如图1,A、B是直线![]() 同旁的两个定点.
同旁的两个定点.
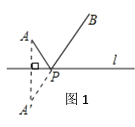
问题:在直线![]() 上确定一点P,使PA+PB的值最小.
上确定一点P,使PA+PB的值最小.
方法:作点A关于直线![]() 的对称点A′,连接A′B交
的对称点A′,连接A′B交![]() 于点P,则PA+PB=A′B的值最小(不必证明).
于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图2,已知平面直角坐标系中两定点A(0,-1),B(2,-1),P为x轴上一动点, 则当PA+PB的值最小时,点P的横坐标是______,此时PA+PB的最小值是______;
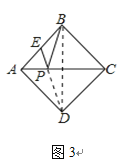
(2)如图3,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.由正方形对称性可知,B与D关于直线AC对称,连接BD,则PB+PE的最小值是______;
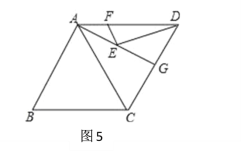
(3)如图4,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一动点P,则PD+PE的最小值为 ;
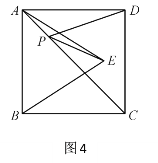
(4)如图5,在菱形ABCD中,AB=8,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,围成长方形的花圃,且花圃的一边为墙体(墙体的最大可用长度为20m)。
设花圃的面积为![]() AB的长为xm.
AB的长为xm.
(1)求y与x函数关系式,并写出x的取值范围;
(2)x为何值时,y取得最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据农业农村部消息,国内受猪瘟与猪周期叠加影响,生猪供应量大幅减少,从今年6月起猪肉价格连续上涨一品生鲜超市在6月1日若售出![]() 五花肉和
五花肉和![]() 排骨,销售额为366元;若售出
排骨,销售额为366元;若售出![]() 五花肉和
五花肉和![]() 排骨,销售额为186元.
排骨,销售额为186元.
(1)6月1日每千克五花肉和排骨的价格各是多少元?
(2)6月1日五花肉和排骨的销售量分别为![]() 、
、![]() 由于猪肉价格持续上涨,11月1日五花肉的销售价格在6月1日的基础上增长了
由于猪肉价格持续上涨,11月1日五花肉的销售价格在6月1日的基础上增长了![]() ,销售量减少了
,销售量减少了![]() ;排骨的销售价格在6月1日的基础上增加了
;排骨的销售价格在6月1日的基础上增加了![]() 元,销售量下降了
元,销售量下降了![]() .结果1l月1日的销售额比6月1日的销售额多5100元,求
.结果1l月1日的销售额比6月1日的销售额多5100元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2台大收割机和5台小收割机同时工作2 h共收割小麦3.6hm2,3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com