
����Ŀ������ģ�ͣ�
��������ͼ1��A��B��ֱ��![]() ͬ�Ե��������㣮
ͬ�Ե��������㣮
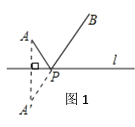
���⣺��ֱ��![]() ��ȷ��һ��P��ʹPA+PB��ֵ��С��
��ȷ��һ��P��ʹPA+PB��ֵ��С��
����������A����ֱ��![]() �ĶԳƵ�A��������A��B��
�ĶԳƵ�A��������A��B��![]() �ڵ�P����PA+PB=A��B��ֵ��С������֤������
�ڵ�P����PA+PB=A��B��ֵ��С������֤������
ģ��Ӧ�ã�
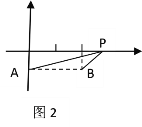
��1����ͼ2,��֪ƽ��ֱ������ϵ��������A��0��-1����B��2��-1��,PΪx����һ����, ��PA+PB��ֵ��Сʱ����P�ĺ�������______����ʱPA+PB����Сֵ��______��
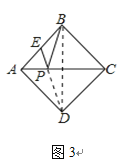
��2����ͼ3��������ABCD�ı߳�Ϊ2��EΪAB���е㣬P��AC��һ����.�������ζԳ��Կ�֪��B��D����ֱ��AC�Գƣ�����BD����PB+PE����Сֵ��______��
��3����ͼ4,������ABCD�����Ϊ12����ABE�ǵȱ������Σ���E��������ABCD�ڣ��ڶԽ���AC����һ����P����PD��PE����СֵΪ ��
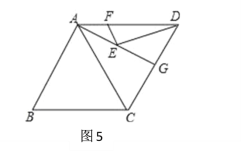
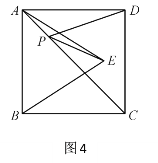
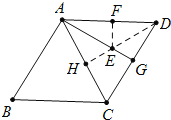
��4����ͼ5,������ABCD�У�AB=8����B=60������G�DZ�CD�ߵ��е㣬��E��F�ֱ���AG��AD�ϵ��������㣬��EF+ED����Сֵ��_______________.
���𰸡���1����P�ĺ������� 1 ����ʱPA+PB����Сֵ��![]() ����2��PB+PE����Сֵ��
����2��PB+PE����Сֵ��![]() ��3�������СֵΪ
��3�������СֵΪ ![]() ����4��EF+ED����Сֵ��
����4��EF+ED����Сֵ��![]()
��������
��1��ȡ��A����x��ԳƵĵ�A��������A��B����x����P����BH��x����H�����OP���õ���P�ĺ����꣬���ݹ��ɶ������A��B���õ��𰸣�
��2����������PB+PE=PD+PE=DE������ADE�У����ݹ��ɶ�����ü��ɣ�
��3�����ڵ�B��D����AC�Գƣ���������BD����AC�Ľ��㼴ΪF�㣮��ʱPD+PE=BE��С����BE�ǵȱ���ABE�ıߣ�BE=AB����������ABCD�����Ϊ12�������AB�ij����Ӷ��ó������
��4����DH��AC����ΪH��AG���ڵ�E����H����AG�ĶԳƵ�ΪF����ʱEF+ED��С=DH����֤����ADC�ǵȱ������Σ���RT��DCH�����ù��ɶ������ɽ�����⣮
��1��ȡ��A����x��ԳƵĵ�A��������A��B����x����P����BH��x����H��
���ʱPA+PB��ֵ��С��

��OA��=OA=1��BH=1��BH��OA����
��OP=PH=1��
���P�������1��
PA+PB=A��B=![]() ��
��
�ʴ�Ϊ��1��2![]() ��
��
��2�����ı���ABCD�������Σ�
��AC��ֱƽ��BD��
��PB=PD��
�������ã�PB+PE=PD+PE=DE��
����ADE�У����ݹ��ɶ����ã�DE=![]() ��
��
��3������BD����AC���ڵ�F��

�ߵ�B��D����AC�Գƣ�
��PD=PB��
��PD+PE=PB+PE=BE����
��������ABCD�����Ϊ12��
��AB=2![]() ��
��
�֡ߡ�ABE�ǵȱ������Σ�
��BE=AB=2![]() ��
��
��������СֵΪ2![]() ��
��
��4����ͼ��DH��AC����ΪH��AG���ڵ�E��
���ı���ABCD�����Σ�
��AB=AD=CD=BC=8��
�ߡ�B=60����
���ADC=��B=60����
���ADC�ǵȱ������Σ�
��AG�����ߣ�
���GAD=��GAC
���H����AG�ĶԳƵ�F��AD�ϣ���ʱEF+ED��С=DH��
��RT��DHC�У��ߡ�DHC=90����DC=6��![]() ��ADC=30����
��ADC=30����
��CH=![]() DC=4��DH=
DC=4��DH=![]() ��
��
��EF+DE����Сֵ=DH=4![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¶���һ�������Σ�����ƽ���͵��ڵ�����ƽ���������������ν������������Σ�
��1���������������������Ķ��壬�����ж��������ȱ�������һ������������������������Ǽ�����?
��2����Rt��ABC�У���ACB=90����AB=c��AC=b��BC=a����b��a����Rt��ABC�����������Σ���a��b��c��
��3����ͼ��AB����O��ֱ������C����O��һ�㣨�����A��B�غϣ���D�ǰ�Բ![]() ���е㣬C��D��ֱ��AB�����࣬������O�ڴ��ڵ�E��ʹAE=AD��CB=CE��
���е㣬C��D��ֱ��AB�����࣬������O�ڴ��ڵ�E��ʹAE=AD��CB=CE��
��֤����ACE�����������Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ŀڴ���װ�к졢�ơ���������ɫ��С����ɫ��ͬ�⣬������һ���������к���2��������1�������ڴ�����������һ������ĸ���Ϊ![]() ��
��
��1������л���ĸ�����
��2����һ������һ�����Żأ����ڶ���������һ����������״ͼ���б��������������Ķ��Ǻ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
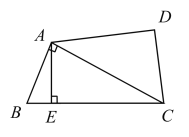
����Ŀ����ͼ��������ABCD�У�AE��BC��E������ABE��AE����ֱ�߷��۵���AEF����AB��2����B��45��������AEF������ABCD�ص����֣���Ӱ���֣������Ϊ�� ��.
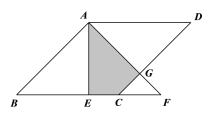
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��![]() ��
��![]() ������Ʒ������1��
������Ʒ������1��![]() ��Ʒ�ȹ���1��
��Ʒ�ȹ���1��![]() ��Ʒ�10Ԫ�����һ���300Ԫ����
��Ʒ�10Ԫ�����һ���300Ԫ����![]() ��Ʒ�ͻ���100Ԫ����
��Ʒ�ͻ���100Ԫ����![]() ��Ʒ��������ȣ�
��Ʒ��������ȣ�
��1������һ��![]() ��Ʒ��һ��
��Ʒ��һ��![]() ��Ʒ����Ҫ����Ԫ��
��Ʒ����Ҫ����Ԫ��
��2���̵�������![]() ��
��![]() ������Ʒ��80������
������Ʒ��80������![]() ��Ʒ������������
��Ʒ������������![]() ��Ʒ������4�������ҹ���
��Ʒ������4�������ҹ���![]() ��
��![]() ��Ʒ���ܷ��ò�����1000Ԫ�Ҳ�����1050Ԫ����ô�̵����ļ��ֹ�����
��Ʒ���ܷ��ò�����1000Ԫ�Ҳ�����1050Ԫ����ô�̵����ļ��ֹ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
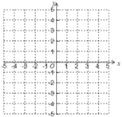
����Ŀ����֪���κ���y=��x2+2x+3��
��1�����俪�ڷ��Գ��ᡢ�������꣬���������������ͼ����
��2������ͼ��ֱ��д�����ٵ�����ֵyΪ����ʱ���Ա���x��ȡֵ��Χ��
�ڵ���2��x��2ʱ������ֵy��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
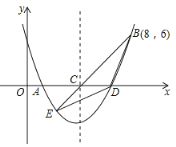
����Ŀ����ͼ�����κ���y=![]() x2+bx+c��ͼ��x����A��D���㲢����B�㣬��֪A�������ǣ�2��0����B��������ǣ�8��6����
x2+bx+c��ͼ��x����A��D���㲢����B�㣬��֪A�������ǣ�2��0����B��������ǣ�8��6����
��1������κ����Ľ���ʽ��
��2������ͼ��Ķ������꼰D���������
��3���ö��κ����ĶԳ��ύx����C�㣬����BC�����ӳ�BC����������E�㣬����BD��DE�����BDE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ���߳�Ϊ
���߳�Ϊ![]() �����������ε�һ�߾���ͬһֱ���ϣ���
�����������ε�һ�߾���ͬһֱ���ϣ���![]() ��
��![]() ��
��![]() ����
����![]() �ֱ�Ϊ��
�ֱ�Ϊ��![]() ��
��![]() ��
��![]() ������
������![]() ���е㣬
���е㣬![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() �����Ϊ
�����Ϊ![]() ����
����![]() ________�����ú�
________�����ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С����һ���ı��οյ�![]() ������
������![]() .Ϊ��Ӧɳ�����ģ�����С���ĺ��٣�С���ƻ�������ı��οյؽ��й滮����.����
.Ϊ��Ӧɳ�����ģ�����С���ĺ��٣�С���ƻ�������ı��οյؽ��й滮����.����![]() ���˴�ֱ��
���˴�ֱ��![]() ��С·
��ѷ![]() .��������
.��������![]() ��
��![]() ��
��![]() .
.
��1�������յ�![]() �������
�������
��2����С·![]() �ij�.���𰸿ɺ����ţ�
�ij�.���𰸿ɺ����ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com