
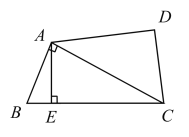
【题目】如图,小区有一块四边形空地![]() ,其中
,其中![]() .为响应沙区创文,美化小区的号召,小区计划将这块四边形空地进行规划整理.过点
.为响应沙区创文,美化小区的号召,小区计划将这块四边形空地进行规划整理.过点![]() 作了垂直于
作了垂直于![]() 的小路
的小路![]() .经测量,
.经测量,![]() ,
,![]() ,
,![]() .
.
(1)求这块空地![]() 的面积;
的面积;
(2)求小路![]() 的长.(答案可含根号)
的长.(答案可含根号)
 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
【题目】几何模型:
条件:如图1,A、B是直线![]() 同旁的两个定点.
同旁的两个定点.
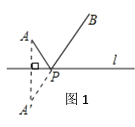
问题:在直线![]() 上确定一点P,使PA+PB的值最小.
上确定一点P,使PA+PB的值最小.
方法:作点A关于直线![]() 的对称点A′,连接A′B交
的对称点A′,连接A′B交![]() 于点P,则PA+PB=A′B的值最小(不必证明).
于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
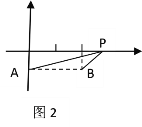
(1)如图2,已知平面直角坐标系中两定点A(0,-1),B(2,-1),P为x轴上一动点, 则当PA+PB的值最小时,点P的横坐标是______,此时PA+PB的最小值是______;
(2)如图3,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.由正方形对称性可知,B与D关于直线AC对称,连接BD,则PB+PE的最小值是______;
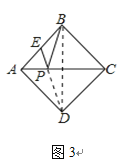
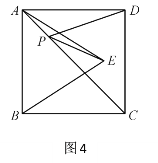
(3)如图4,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一动点P,则PD+PE的最小值为 ;
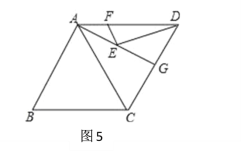
(4)如图5,在菱形ABCD中,AB=8,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据农业农村部消息,国内受猪瘟与猪周期叠加影响,生猪供应量大幅减少,从今年6月起猪肉价格连续上涨一品生鲜超市在6月1日若售出![]() 五花肉和
五花肉和![]() 排骨,销售额为366元;若售出
排骨,销售额为366元;若售出![]() 五花肉和
五花肉和![]() 排骨,销售额为186元.
排骨,销售额为186元.
(1)6月1日每千克五花肉和排骨的价格各是多少元?
(2)6月1日五花肉和排骨的销售量分别为![]() 、
、![]() 由于猪肉价格持续上涨,11月1日五花肉的销售价格在6月1日的基础上增长了
由于猪肉价格持续上涨,11月1日五花肉的销售价格在6月1日的基础上增长了![]() ,销售量减少了
,销售量减少了![]() ;排骨的销售价格在6月1日的基础上增加了
;排骨的销售价格在6月1日的基础上增加了![]() 元,销售量下降了
元,销售量下降了![]() .结果1l月1日的销售额比6月1日的销售额多5100元,求
.结果1l月1日的销售额比6月1日的销售额多5100元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
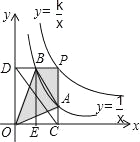
【题目】两个反比例函数y=![]() (k>1)和y=
(k>1)和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B,BE⊥x轴于点E,当点P在y=
的图象于点B,BE⊥x轴于点E,当点P在y=![]() 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化:④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____.(填序号)
图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化:④△OBA的面积等于四边形ACEB的面积.其中一定正确的是_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为选拔一名选手参加“美丽邵阳,我为家乡做代言”主题演讲比赛,经研究,按图所示的项目和权数对选拔赛参赛选手进行考评(因排版原因统计图不完整).下表是李明、张华在选拔赛中的得分情况:
项目 选手 | 服装 | 普通话 | 主题 | 演讲技巧 |
李明 | 85 | 70 | 80 | 85 |
张华 | 90 | 75 | 75 | 80 |
结合以上信息,回答下列问题:
(1)求服装项目的权数及普通话项目对应扇形的圆心角大小;
(2)求李明在选拔赛中四个项目所得分数的众数和中位数;
(3)根据你所学的知识,帮助学校在李明、张华两人中选择一人参加“美丽邵阳,我为家乡做代言”主题演讲比赛,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学测试中,同年级人数相同的甲、乙两个班的成绩统计如下表:
班级 | 平均分 | 中位数 | 方差 |
甲班 |
|
|
|
乙班 |
|
|
|
数学老师让同学们针对统计的结果进行一下评估,学生的评估结果如下:
![]() 这次数学测试成绩中,甲、乙两个班的平均水平相同;
这次数学测试成绩中,甲、乙两个班的平均水平相同;
![]() 甲班学生中数学成绩95分及以上的人数少;
甲班学生中数学成绩95分及以上的人数少;
![]() 乙班学生的数学成绩比较整齐,分化较小.
乙班学生的数学成绩比较整齐,分化较小.
上述评估中,正确的是______![]() 填序号
填序号![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2台大收割机和5台小收割机同时工作2 h共收割小麦3.6hm2,3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, AD是∠BAC的平分线,DF⊥AB,DM⊥AC,垂足分别为F、M,AF=10cm ,BF=6cm ,AC=14cm.动点E以3cm/s的速度从A点向B点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t s.当t=__________s时, △DFE与△DMG全等.(写出符合题意的t的所有取值)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△AOB中,∠AOB=90°,AO=3cm,BO=4cm,将△AOB绕顶点O,按顺时针方向旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段B1D的长度为( )
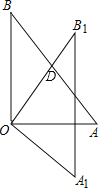
A.![]() cmB.1cmC.2cmD.
cmB.1cmC.2cmD.![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com