
【题目】如图,在平面直角坐标系中,⊙P与y轴相切,交直线y=x于A,B两点,已知圆心P的坐标为(2,a)(a>2),AB=2 ![]() ,则a的值为( )
,则a的值为( ) 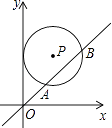
A.4
B.2+ ![]()
C.![]()
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b在数轴上的对应点如图所示,则下列式子中错误的是( )
![]()
A. a+b<0 B. a-b<0
C. -a<-b D. |a-b|=b-a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】基本模型:如图1,点A,F,B在同一直线上,若∠A=∠B=∠EFC=90°,易得△AFE~△BCF. 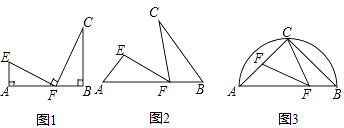
(1)模型拓展:如图2,点A,F,B在同一直线上,若∠A=∠B=∠EFC,求证:△AFE~△BCF;
(2)拓展应用:如图3,AB是半圆⊙O的直径,弦长AC=BC=4 ![]() ,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
,E,F分别是AC,AB上的一点,若∠CFE=45°,若设AE=y,BF=x,求y与x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过y轴上一点P(0,1)作平行于x轴的直线PB,分别交函数y1=x2(x≥0)与y2= ![]() (x≥0)的图象于A1 , B1两点,过点B1作y轴的平行线交y1的图象于点A2 , 再过A2作直线A2B2∥x轴,交y2的图象于点B2 , 依次进行下去,连接A1A2 , B1B2 , A2A3 , B2B3 , …,记△A2A1B1的面积为S1 , △A2B1B2的面积为S2 , △A3A2B2的面积为S3 , △A3B2B3的面积为S4 , …则S2016=
(x≥0)的图象于A1 , B1两点,过点B1作y轴的平行线交y1的图象于点A2 , 再过A2作直线A2B2∥x轴,交y2的图象于点B2 , 依次进行下去,连接A1A2 , B1B2 , A2A3 , B2B3 , …,记△A2A1B1的面积为S1 , △A2B1B2的面积为S2 , △A3A2B2的面积为S3 , △A3B2B3的面积为S4 , …则S2016= 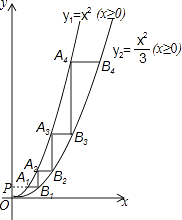
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线y=2x+m与y轴交于点A,与直线y=-x+5交于点B(4,n),P为直线y=-x+5上一点.
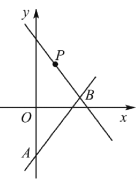
(1)求m,n的值;
(2)求线段AP的最小值,并求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,义乌市某服装厂每件衣服原材料的成本y1(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本y2(元)与月份x的函数关系式为y2=x+62(8≤x≤12,且x为整数).
(1)请观察表格中的数据,用学过的函数相关知识求y1与x的函数关系式.
(2)若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量p2(万件)与月份x满足关系式p2=﹣0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com