
【题目】如图,点A、B和线段MN都在数轴上,点A、M、N、B对应的数字分别为﹣1、0、2、11.线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.
(1)用含有t的代数式表示AM的长为
(2)当t= 秒时,AM+BN=11.
(3)若点A、B与线段MN同时移动,点A以每秒2个单位速度向数轴的正方向移动,点B以每秒1个单位的速度向数轴的负方向移动,在移动过程,AM和BN可能相等吗?若相等,请求出t的值,若不相等,请说明理由.
![]()
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】分析:(1)根据点M开始表示的数结合其运动速度和时间,即可得出运动后点M的表示的数,再依据点A表示的数为-1即可得出结论;(2)分别找出AM、BN,根据AM+BN=11即可列出关于t的含绝对值符号的一元一次方程,解方程即可得出结论;
(3)假设能够相等,找出AM、BN,根据AM=BN即可列出关于t的含绝对值符号的一元一次方程,解方程即可得出结论.
本题解析:(1)∵点A、M、N对应的数字分别为﹣1、0、2,线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒,
∴移动后M表示的数为t,N表示的数为t+2,
∴AM=t﹣(﹣1)=t+1.
(2)由(1)可知:BN=|11﹣(t+2)|=|9﹣t|,
∵AM+BN=11,
∴t+1+|9﹣t|=11,
解得: ![]()
(3)假设能相等 ,则点A表示的数为2t﹣1,M表示的数为t,N表示的数为t+2,B表示的数为11﹣t,
∴AM=|2t﹣1﹣t|=|t﹣1|,BN=|t+2﹣(11﹣t)|=|2t﹣9|,
∵AM=BN,
∴|t﹣1|=|2t﹣9|,
![]()
故在运动的过程中AM和BN能相等,此时运动的时间为 秒和8秒.


科目:初中数学 来源: 题型:
【题目】已知点A、B在数轴上表示的数分别为m、n.
(1)对照数轴完成下表:

(2)若A、B两点间的距离为d,试写出d与m、n之间数量关系,并用文字语言描述
这个数量关系;
(3)已知A、B两点在数轴上表示的数分别为x和-2,则A、B两点的距离d可表示
为 ;如果d=3,求x的值。
(4)若数轴上表示数m的点位于表示数-5和3的点之间,求|m+5|+|m-3|的值(用含x的式子表示);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足|a﹣![]() |+
|+![]() +(c﹣4
+(c﹣4![]() )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l1经过点E(1,0)和F(5,0),并交y轴于D(0,﹣5);抛物线l2:y=ax2﹣(2a+2)x+3(a≠0),
(1)试求抛物线l1的函数解析式;
(2)求证:抛物线 l2与x轴一定有两个不同的交点;
(3)若a=1,抛物线l1、l2顶点分别为、;当x的取值范围是时,抛物线l1、l2 上的点的纵坐标同时随横坐标增大而增大;
(4)若a=1,已知直线MN分别与x轴、l1、l2分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式A=x2+3xy+x-![]() ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1
(1)当x=y=-2时,求2A-B的值;
(2)若2A-B的值与y的取值无关,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.

图① 图② 图③
证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)
【变式探究】
当点P在CB延长线上时,其余条件不变(如图3).试探索PD、PE、CF之间的数量关系并说明理由.
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】
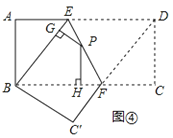
如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】
在直角坐标系中.直线l1:y=![]() 与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.
与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.
(1)求证:EF=DF﹣BE;
(2)若△ADF的周长为![]() ,求EF的长.
,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com