
| A. | ($\frac{2{a}^{-3}b}{-{c}^{3}}$)2=$\frac{4{a}^{9}b}{{c}^{5}}$ | B. | ($\frac{2x-y}{-5{a}^{2}}$)2=$\frac{4{x}^{2}-{y}^{2}}{25{a}^{4}}$ | ||
| C. | (3xny-n)-m=$\frac{{y}^{mn}}{{3}^{m}x^{mn}}$ | D. | (-$\frac{{b}^{2}}{a}$)2n=-$\frac{{b}^{2+2n}}{{a}^{n}}$ |
分析 根据分式的乘方:($\frac{a}{b}$)n=$\frac{{a}^{n}}{{b}^{n}}$,可得负整数指数幂,根据负整数指数幂与正整数指数幂互为倒数即可求解.
解答 解:A、($\frac{2{a}^{-3}b}{-{c}^{3}}$)2=$\frac{4{a}^{-6}{b}^{2}}{{c}^{6}}$=$\frac{4{b}^{2}}{{a}^{6}{c}^{6}}$,故A错误;
B、($\frac{2x-y}{-5{a}^{2}}$)2=$\frac{(2x-y)^{2}}{25{a}^{4}}$,故B错误;
C、(3xny-n)-m=3-mx-mnymn=$\frac{{y}^{mn}}{{3}^{m}{x}^{mn}}$,故C正确;
D、(-$\frac{{b}^{2}}{a}$)2n=$\frac{{b}^{4n}}{{a}^{2n}}$,故D错误.
故选:C.
点评 本题考查了负整数指数幂,利用分式的乘方:($\frac{a}{b}$)n=$\frac{{a}^{n}}{{b}^{n}}$,负整数指数幂与正整数指数幂互为倒数是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
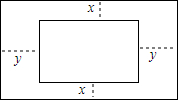 姥姥有一张长2米、宽1米的十字绣,她在十字绣的四周加上了花边做成了挂毯,上下花边宽度为x米,左右花边宽度为y米,若十字绣与挂毯是相似的长方形.
姥姥有一张长2米、宽1米的十字绣,她在十字绣的四周加上了花边做成了挂毯,上下花边宽度为x米,左右花边宽度为y米,若十字绣与挂毯是相似的长方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
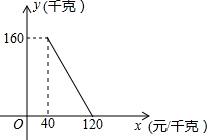 某商店以40元/千克的单价新近一批茶叶,经调查发现,在一段时间内,销量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
某商店以40元/千克的单价新近一批茶叶,经调查发现,在一段时间内,销量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com