
【题目】如图,矩形ABCD中,AB=10,AD=4,点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的左上方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当点F落在直线MN上,设运动的时间为t,则t的值为( )

A.1B.![]() C.4D.
C.4D.![]()
【答案】D
【解析】
过点F作FH⊥CD,交直线CD于点Q,则∠EHF=90°,易证∠ADE=∠EHF,由正方形的性质得出∠AEF=90°,AE=EF,证得∠AED=∠EFH,由AAS证得△ADE≌△EHF得出AD=EH=4,则t+2t=4+10,即可得出结果.
过点F作FH⊥CD,交直线CD于点Q,则∠EHF=90°,如图所示:
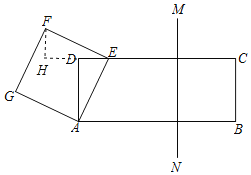
∵四边形ABCD为矩形,
∴∠ADE=90°,
∴∠ADE=∠EHF,
∵在正方形AEFG中,∠AEF=90°,AE=EF,
∴∠AED+∠HEF=90°,
∵∠HEF+∠EFH=90°,
∴∠AED=∠EFH,
在△ADE和△EHF中,
 ,
,
∴△ADE≌△EHF(AAS),
∴AD=EH=4,
由题意得:t+2t=4+10,
解得:t=![]() ,
,
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=45°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )

A.①②③B.②③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为贫困山区捐款,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
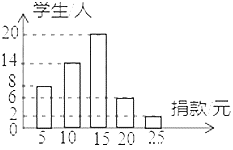
![]() 这50名同学捐款的众数为______元,中位数为______元;
这50名同学捐款的众数为______元,中位数为______元;
![]() 求这50名同学捐款的平均数_______元;
求这50名同学捐款的平均数_______元;
![]() 该校共有1200名学生参与捐款,请估计该校学生的捐款总钱数.
该校共有1200名学生参与捐款,请估计该校学生的捐款总钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
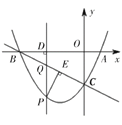
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上的一个动点,过
是抛物线上的一个动点,过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)直接写出![]() ,
,![]() ,
,![]() 三点的坐标;
三点的坐标;
(2)若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求此时点
为顶点的四边形是平行四边形,求此时点![]() 的坐标;
的坐标;
(3)当点![]() 位于直线
位于直线![]() 下方的抛物线上时,过点
下方的抛物线上时,过点![]() 作
作![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求
的函数关系式,并求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列14×7的网格中,横、纵坐标均为整点的数叫做格点,例如A(-6,0)、B(-3,4)都是格点.
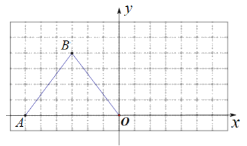
(1)直接写出△ABO的形状;
(2)要求在下图中仅用无刻度的直尺作图:将△ABO绕点O顺时针旋转得△DEO,且点B的对应点E落在x轴正半轴上.操作如下:
第一步:在x正半轴上找一个格点E,使OE=OB;
第二步:找一个格点F,使∠EOF=∠AOB;
第三步:找一个格点M,作直线长AM交直线OF于D,连DE,则△DEO即为所作出的图形.
请你按步骤完成作图,并直接写出直线AM的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C地在B地的正东方向,因有大山阻隔,由B地到C地需绕行A地,已知A地位于B地北偏东67°方向,距离B地520km,C地位于A地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求建成高铁后从B地前往C地的路程.(![]() ,结果保留整数)
,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
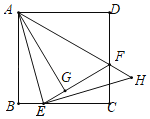
【题目】如图,已知正方形ABCD的边长为3,E是边BC上一点,BE=1,将△ABE,△ADF分别沿折痕AE,AF向内折叠,点B,D在点G处重合,过点E作EH⊥AE,交AF的延长线于H,则线段FH的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com