
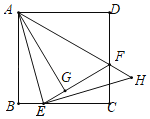
【题目】如图,已知正方形ABCD的边长为3,E是边BC上一点,BE=1,将△ABE,△ADF分别沿折痕AE,AF向内折叠,点B,D在点G处重合,过点E作EH⊥AE,交AF的延长线于H,则线段FH的长为_______.
【答案】![]()
【解析】
设DF=FG=x,在Rt△EFC中,由EF=1+x,EC=3﹣1=2,FC=3﹣x,根据勾股定理构建方程求出x,再求出AF,AH即可解决问题.
解:∵四边形ABCD是正方形,
∴∠B=∠C=∠D=∠BAD=90°,AB=BC=CD=AD=3,
设DF=FG=x,
在Rt△EFC中,∵EF=1+x,EC=3﹣1=2,FC=3﹣x,
∴(x+1)2=22+(3﹣x)2,
解得x=![]()
∴AF=![]() =
= =
=![]() ,AE=
,AE=![]() =
=![]() =
=![]() ,
,
由翻折的性质可知,∠DAF=∠GAF,∠EAB=∠EAG,
∴∠EAH=45°,
∵EH⊥EA,
∴∠AEH=90°,
∴AE=EH=![]() ,AH=
,AH=![]() AE=2
AE=2![]() ,
,
∴FH=AH﹣AF=2![]() ﹣
﹣![]() =
=![]() ,
,
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线y=![]() x2+bx+c经过点A(-1,0),B(5,0).
x2+bx+c经过点A(-1,0),B(5,0).

(1)求抛物线的解析式并写出顶点M的坐标;
(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下统计图:

(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为___________度
(2)请补充完整下面的成绩统计分析表:
平均数 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 |
|
乙组 | 1.36 |
|
(3)你认为那组成绩较好?从以上信息中写出两条支持你的选择
(4)从甲、乙两组得9分的学生中抽取两人参加市级比赛,求这两人来自不同组的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=10,AD=4,点E从D向C以每秒1个单位的速度运动,以AE为一边在AE的左上方作正方形AEFG,同时垂直于CD的直线MN也从C向D以每秒2个单位的速度运动,当点F落在直线MN上,设运动的时间为t,则t的值为( )

A.1B.![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径作圆交AC、BC于点D、E两点,AF切⊙O于点A,点D是AC中点.

(1)求证:AB=BC;
(2)若![]() ,CF=
,CF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承接一铁路工程,在挖掘一条500米长的隧道时,为了尽快完成,实际施工时每天挖掘的长度是原计划的1.5倍,结果提前了25天完成了其中300米的隧道挖掘任务.
(1)求实际每天挖掘多少米?
(2)由于气候等原因,需要进一步缩短工期,要求完成整条隧道不超过70天,那么为了完成剩下的任务,在实际每天挖掘长度的基础上,至少每天还应多挖掘多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和爸爸登山,两人距地面的高度![]() (米)与小亮登山时间
(米)与小亮登山时间![]() (分)之间的函数图象分别如图中折线
(分)之间的函数图象分别如图中折线![]() 和线段
和线段![]() 所示,根据函数图形进行一下探究:
所示,根据函数图形进行一下探究:

(1)设线段![]() 所表示的函数关系式为
所表示的函数关系式为![]() ,根据图象求
,根据图象求![]() 的值,并写出
的值,并写出![]() 的实际意义;
的实际意义;
(2)若小亮提速后,他登山的速度是爸爸速度的3倍,问:小亮登山多长时间时开始提速?此时小亮距地面的高度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,其中
两点,其中![]() ,
,![]() .该抛物线与
.该抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() .
.

(1)求![]() 的值及该抛物线的解析式;
的值及该抛物线的解析式;
(2)如图2.若点![]() 为线段
为线段![]() 上的一动点(不与
上的一动点(不与![]() 重合).分别以
重合).分别以![]() 、
、![]() 为斜边,在直线
为斜边,在直线![]() 的同侧作等腰直角△
的同侧作等腰直角△![]() 和等腰直角△
和等腰直角△![]() ,连接
,连接![]() ,试确定△
,试确定△![]() 面积最大时
面积最大时![]() 点的坐标.
点的坐标.
(3)如图3.连接![]() 、
、![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,若存在,请直接写出点
相似,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com