
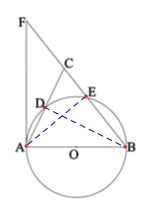
【题目】如图,在△ABC中,以AB为直径作圆交AC、BC于点D、E两点,AF切⊙O于点A,点D是AC中点.

(1)求证:AB=BC;
(2)若![]() ,CF=
,CF=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)半径为![]() .
.
【解析】
(1)连接BD,易证BD⊥AC,结合点D是AC中点,即可得到结论;
(2)连接AE,设CE=![]() ,则AC=4k,CD=2k,由CAE~CBD,得
,则AC=4k,CD=2k,由CAE~CBD,得![]() ,从而得BC=
,从而得BC=![]() ,BE=
,BE=![]() ,由AEF~BEA,得
,由AEF~BEA,得![]() ,结合
,结合![]() ,得k=
,得k=![]() ,进而即可求解.
,进而即可求解.
(1)连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,即:BD⊥AC,
又∵点D是AC中点,
∴BD是AC的中垂线,
∴AB=BC;
(2)连接AE,
∵![]() ,
,
∴设CE=![]() ,则AC=4k,
,则AC=4k,
∵点D是AC中点,
∴CD=![]() AC=2k,
AC=2k,
∵AB是⊙O的直径,
∴∠AEC=∠BDC=90°,
又∵∠CAE=∠CBD,
∴CAE~CBD,
∴![]() ,即:
,即:![]() ,
,
∴BC=![]() ,BE=
,BE=![]() -
-![]() =
=![]() ,
,
∵AF切⊙O于点A,
∴AB⊥AF,
∴∠FAE+∠BAE=∠EAB+∠ABE=90°,
∴∠FAE=∠ABE,
∵∠AEF=∠BEA=90°,
∴AEF~BEA,
∴![]() ,即:
,即:![]() ,
,
又∵![]() , CF=
, CF=![]() ,
,
∴![]() ,解得:k=
,解得:k=![]() ,
,
∴![]() ,BE=
,BE=![]() =
=![]() ,
,
∴![]() ,
,
∴⊙O的半径为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在“阳光体育”活动时间,小英、小丽、小敏、小洁四位同学进行一次羽毛球单打比赛,要从中选出两位同学打第一场比赛.
(1)若已确定小英打第一场,再从其余三位同学中随机选取一位,求恰好选中小丽同学的概率;
(2)用画树状图或列表的方法,求恰好选中小敏、小洁两位同学进行比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为xh,两车之间的距离为ykm,图中的折线表示y与x之间的函数关系,根据图象解决以下问题:
(1)慢车的速度为_____km/h,快车的速度为_____km/h;
(2)解释图中点C的实际意义并求出点C的坐标;
(3)求当x为多少时,两车之间的距离为500km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列14×7的网格中,横、纵坐标均为整点的数叫做格点,例如A(-6,0)、B(-3,4)都是格点.
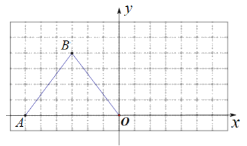
(1)直接写出△ABO的形状;
(2)要求在下图中仅用无刻度的直尺作图:将△ABO绕点O顺时针旋转得△DEO,且点B的对应点E落在x轴正半轴上.操作如下:
第一步:在x正半轴上找一个格点E,使OE=OB;
第二步:找一个格点F,使∠EOF=∠AOB;
第三步:找一个格点M,作直线长AM交直线OF于D,连DE,则△DEO即为所作出的图形.
请你按步骤完成作图,并直接写出直线AM的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
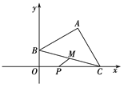
【题目】在平面直角坐标系中,点C、B分别在![]() 轴、
轴、![]() 轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
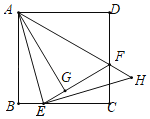
【题目】如图,已知正方形ABCD的边长为3,E是边BC上一点,BE=1,将△ABE,△ADF分别沿折痕AE,AF向内折叠,点B,D在点G处重合,过点E作EH⊥AE,交AF的延长线于H,则线段FH的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在试销一种进价为20元/件的商品时,每天不断调整该商品的售价以期获利更多,经过20天的试销发现,第一天销售量为78件,以后每天销售量总比前一天减少2件,且第1天至第10天,商品销售单价p与天数x满足:p=30+x;第11天至第20天,商品销售单价p与天数x满足:p=20+![]() .
.
(1)写出销售量y(件)与天数x(天)的函数关系式;
(2)求商场销售该商品的20天里每天获得的利润w(元)与x的函数关系式;
(3)该商品试制期间,第几天销售该商品获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天来了,我校计划组织师生共![]() 人坐
人坐![]() 、
、![]() 两种型号的大巴车外出春游,且
两种型号的大巴车外出春游,且![]() 型车每辆租金为
型车每辆租金为![]() 元,
元,![]() 型车每辆租金为
型车每辆租金为![]() 元,为了保证安全,校方要求必须保证人人都有座位.学生南南发现若租
元,为了保证安全,校方要求必须保证人人都有座位.学生南南发现若租![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车恰好能坐下
型大巴车恰好能坐下![]() 人,若租
人,若租![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车恰好能坐下
型大巴车恰好能坐下![]() 人.
人.
(1)请问![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车各有几座?
型大巴车各有几座?
(2)现学校决定租两种型号的大巴车共![]() 辆作为出行交通工具,但政教主任蒋老师发现租车总经费不能超过
辆作为出行交通工具,但政教主任蒋老师发现租车总经费不能超过![]() 元.他想运用函数的知识进行分析,为学校寻找最节省的租车方案.现蒋老师设学校租了
元.他想运用函数的知识进行分析,为学校寻找最节省的租车方案.现蒋老师设学校租了![]() 型大巴车
型大巴车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.请你帮蒋老师完成分析过程,确定共有几种租车方案?哪种租车方案最省钱?并求出最低费用.
元.请你帮蒋老师完成分析过程,确定共有几种租车方案?哪种租车方案最省钱?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
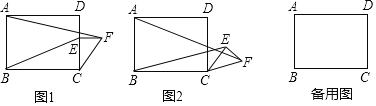
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是边CD上的点,且CE=4,过点E作CD的垂线,并在垂线上截取EF=3,连接CF.将△CEF绕点C按顺时针方向旋转,记旋转角为a.
(1)问题发现
当a=0°时,AF= ,BE= ,![]() = ;
= ;
(2)拓展探究
试判断:当0°≤a°<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△CEF旋转至A,E,F三点共线时,直接写出线段BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com