
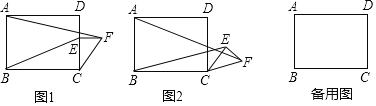
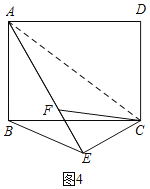
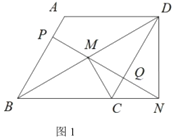
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是边CD上的点,且CE=4,过点E作CD的垂线,并在垂线上截取EF=3,连接CF.将△CEF绕点C按顺时针方向旋转,记旋转角为a.
(1)问题发现
当a=0°时,AF= ,BE= ,![]() = ;
= ;
(2)拓展探究
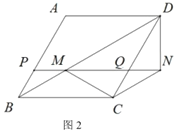
试判断:当0°≤a°<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△CEF旋转至A,E,F三点共线时,直接写出线段BE的长.
【答案】(1)5![]() ,4
,4![]() ,
,![]() ;(2)
;(2)![]() 的大小无变化,理由见解析;(3)BE=
的大小无变化,理由见解析;(3)BE=![]() 或BE=
或BE=![]() .
.
【解析】
(1)根据勾股定理分别计算AF和BE的长可解答;
(2)如图2,连接AC,证明△CEF∽△CBA,得![]() ,再证明△ACF∽△BCE,可解答;
,再证明△ACF∽△BCE,可解答;
(3)当△CEF旋转至A,E,F三点共线时,存在两种情况:连接AC,先计算AF的长,证明△ACF∽△BCE,列比例式可得BE的长.
(1)当a=0°时,如图1,过F作FG⊥AD,交AD的延长线于G,
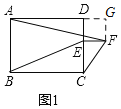
∵四边形ABCD是矩形,
∴∠ADC=∠BCE=90°,AD=BC=8,AB=CD=6,
∵∠G=∠EDG=∠DEF=90°,
∴四边形DEFG是矩形,
∴DG=EF=3,
∴AG=8+3=11,
∵CE=4,CD=6,
∴FG=DE=6﹣4=2,
Rt△AGF中,由勾股定理得:AF=![]() ,
,
Rt△BEC中,由勾股定理得:BE=![]() ,
,
∴![]() ,
,
故答案为![]() ,
,![]() ,
,![]() ;
;
(2)![]() 的大小无变化,理由如下:如图2,连接AC,
的大小无变化,理由如下:如图2,连接AC,
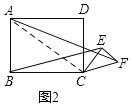
∵AB=6,BC=8,EF=3,CE=4,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵∠CEF=∠ABC=90°,
∴△CEF∽△CBA,
∴![]() ,∠ECF=∠ACB,
,∠ECF=∠ACB,
∴![]() ,
,
∴∠ACF=∠BCE,
∴△ACF∽△BCE,
∴![]() ,即
,即![]() 的大小无变化;
的大小无变化;
(3)当△CEF旋转至A,E,F三点共线时,存在两种情况:
①如图3,连接AC,
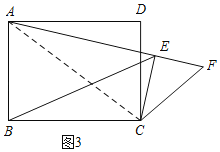
Rt△ABC中,由勾股定理得:AC=![]() =10,
=10,
Rt△CEF中,CE=4,EF=3,
∴CF=5,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵∠FEC=∠ABC,
∴△ABC∽△FEC,
∴∠ACB=∠ECF,
∴∠BCE=∠ACF,
∵![]() ,
,
∴△ACF∽△BCE,
∴![]() ,
,
Rt△AEC中,AE=![]() ,
,
∴AF=AE+EF=![]() +3,
+3,
∴BE=![]() ;
;
②如图4,连接AC,
同理得:△AFC∽△BEC,
∴![]() ,
,
AF=AE﹣EF=![]() ﹣3,
﹣3,
∴BE=![]() ,
,
综上,BE=![]() 或BE=
或BE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径作圆交AC、BC于点D、E两点,AF切⊙O于点A,点D是AC中点.

(1)求证:AB=BC;
(2)若![]() ,CF=
,CF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产基地种植某种食用海藻,从三月一日起的30周内,它的市场价格与上市时间的关系用图①线段表示;它的平均亩产量与时间的关系用图②线段表示;它的每亩平均成本与上市时间的关系用图③抛物线表示.
(1)写出图①、图②所表示的函数关系式;
(2)若市场价×亩产量-亩平均成本 = 每亩总利润,问哪一周上市的海藻利润最大?最大利润是多少?
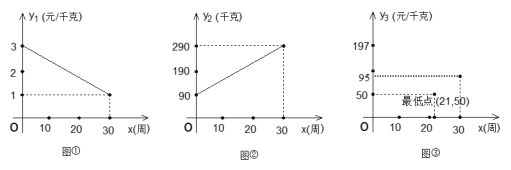
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息解答下列问题:
组别 | 阅读时间 | 频数(人数) |
|
| 8 |
|
| 20 |
|
| 24 |
|
|
|
|
|
|
|
| 4 |
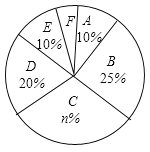
(1)图表中的![]() ______,
______,![]() ______;
______;
(2)扇形统计图中![]() 组所对应的圆心角为______度;
组所对应的圆心角为______度;
(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄石市在创建国家级文明卫生城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,其中
两点,其中![]() ,
,![]() .该抛物线与
.该抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() .
.

(1)求![]() 的值及该抛物线的解析式;
的值及该抛物线的解析式;
(2)如图2.若点![]() 为线段
为线段![]() 上的一动点(不与
上的一动点(不与![]() 重合).分别以
重合).分别以![]() 、
、![]() 为斜边,在直线
为斜边,在直线![]() 的同侧作等腰直角△
的同侧作等腰直角△![]() 和等腰直角△
和等腰直角△![]() ,连接
,连接![]() ,试确定△
,试确定△![]() 面积最大时
面积最大时![]() 点的坐标.
点的坐标.
(3)如图3.连接![]() 、
、![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,若存在,请直接写出点
相似,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
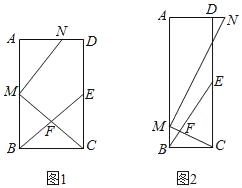
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连接CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)如图1,当点F为BE中点时,求证:AM=CE;
(2)如图2,若![]() =3时,求
=3时,求![]() 的值;
的值;
(3)若![]() =n(n≥3)时,请直接写出
=n(n≥3)时,请直接写出![]() 的值.(用含n的代数式表示)
的值.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点,将线段
上一动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() ,连接
,连接![]() 并延长,分别交
并延长,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(1)如图1,若![]() 且
且![]() ,求菱形
,求菱形![]() 的面积;
的面积;
(2)如图2,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(-1,0);⑤当1<x<4时,有y2<y1,其中正确的是()
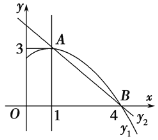
A.①④⑤B.①③④⑤C.①③⑤D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com