
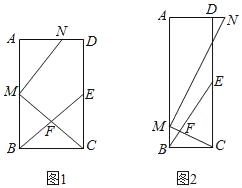
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连接CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)如图1,当点F为BE中点时,求证:AM=CE;
(2)如图2,若![]() =3时,求
=3时,求![]() 的值;
的值;
(3)若![]() =n(n≥3)时,请直接写出
=n(n≥3)时,请直接写出![]() 的值.(用含n的代数式表示)
的值.(用含n的代数式表示)
【答案】(1)见解析;(2)5;(3)![]()
【解析】
(1)由F为BE的中点,可得BF=EF,因为四边形ABCD为矩形,可得∠BCE=∠ABC=90°,CF=BF=EF,∠FBC=∠FCB,可推出△MBC≌△ECB,则可推导出AM=CE.
(2)根据AB∥CD,可得![]() =3,设MB=a,则EC=DE=3a,AB=CD=6a,根据
=3,设MB=a,则EC=DE=3a,AB=CD=6a,根据![]() =3,可得BC=AD=2a,根据MN⊥CM,可推出△AMN∽△BCM,则可得
=3,可得BC=AD=2a,根据MN⊥CM,可推出△AMN∽△BCM,则可得![]() ,
,![]() ,推出AN=
,推出AN=![]() ,DN=
,DN=![]() a,则
a,则![]() =5.
=5.
(3)同(2)的推导方法.
解:(1)∵F为BE的中点,
∴BF=EF,
∵四边形ABCD为矩形,
∴∠BCE=∠ABC=90°,
∴CF=BF=EF,
∴∠FBC=∠FCB,
∵BC=CB,
∴△MBC≌△ECB(AAS),
∴BM=EC=DE,
∵AB=CD,
∴BM=AM,
∴AM=CE.
(2)∵AB∥CD,
∴![]() =3,
=3,
设MB=a,则EC=DE=3a,
∴AB=CD=6a,
∵![]() =3,
=3,
∴BC=AD=2a,
∵MN⊥CM,
∴△AMN∽△BCM,
∴![]() ,
,
∴![]() ,
,
∴AN=![]() ,
,
DN=![]() a,
a,
∴![]() =5.
=5.
(3)∵AB∥CD,
∴![]() =n,
=n,
设MB=a,则EC=DE=an,
∴AB=CD=2an,
∵![]() =n,
=n,
∴BC=AD=2a,
∵MN⊥CM,
∴△AMN∽△BCM,
∴![]() ,
,
∴![]() ,
,
∴AN=![]() ,
,
DN=![]()
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场在试销一种进价为20元/件的商品时,每天不断调整该商品的售价以期获利更多,经过20天的试销发现,第一天销售量为78件,以后每天销售量总比前一天减少2件,且第1天至第10天,商品销售单价p与天数x满足:p=30+x;第11天至第20天,商品销售单价p与天数x满足:p=20+![]() .
.
(1)写出销售量y(件)与天数x(天)的函数关系式;
(2)求商场销售该商品的20天里每天获得的利润w(元)与x的函数关系式;
(3)该商品试制期间,第几天销售该商品获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
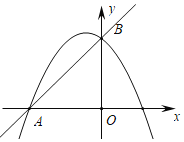
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
(3)如图,当![]() 时,在抛物线上是否存在点
时,在抛物线上是否存在点![]() ,使
,使![]() 的面积为1?若存在,请求出符合条件的所有点
的面积为1?若存在,请求出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
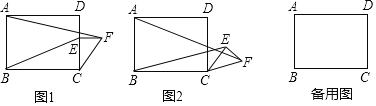
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是边CD上的点,且CE=4,过点E作CD的垂线,并在垂线上截取EF=3,连接CF.将△CEF绕点C按顺时针方向旋转,记旋转角为a.
(1)问题发现
当a=0°时,AF= ,BE= ,![]() = ;
= ;
(2)拓展探究
试判断:当0°≤a°<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△CEF旋转至A,E,F三点共线时,直接写出线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
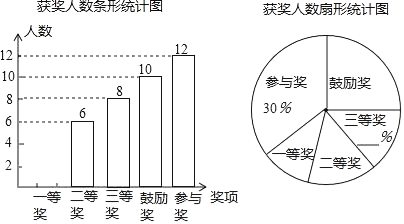
【题目】某校为了接受“省艺术特色学校”的验收,对义务教育的七、八、九三个年级学生举行了书法大赛,赛后对三个年级的获奖情况进行了统计,并绘制了如图所示的两幅不完整的统计图.
请解答下列问题:
(1)请补全两幅统计图;
(2)获得一等奖的同学有![]() 来自七年级,有
来自七年级,有![]() 来自八年级,其余同学均来自九年级.现准备从获得一等奖的同学中任选两人参加市内书法大赛,请你通过列表或画树状图,求所选两人中既有八年级同学又有九年级同学的概率.
来自八年级,其余同学均来自九年级.现准备从获得一等奖的同学中任选两人参加市内书法大赛,请你通过列表或画树状图,求所选两人中既有八年级同学又有九年级同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级全体学生物理实验操作的情况,随机抽取了30名学生的物理实验操作考核成绩,并将数据进行整理,分析如下: (说明:考核成绩均取整数,A级:10分,B级:9分,C级:8分,D级:7分及以下)
收集数据
10,8,10,9,5,10,9,9,10,8,9,10,9,9,8,9,8,10,7,9,8,10,9,6,9,10,9,10,8,10
整理数据
整理、描述样本数据,绘制统计表如下:
抽取的30名学生物理实验操作考核成绩频数统计表
成绩等级 | A | B | C | D |
人数(名) | 10 | m | n | 3 |
根据表中的信息,解答下列问题:
(1)m=________,n=________;
(2)若该校九年级共有800名学生参加物理实验操作考核,成绩不低于9分为优秀,试估计该校九年级参加物理实验操作考核成绩达到优秀的学生有多少名?
(3)甲、乙、丙、丁是九年级1班物理实验考核成绩为10分的四名学生,学校计划从这四名学生中随机选出两名学生代表学校去参加全市中学生“物理实验操作”竞赛,用列表法或画树状图法,求甲、乙两名学生中至少有一名被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
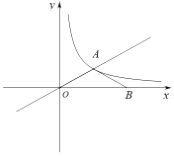
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,正比例函数
为坐标原点,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象都经过点
的图象都经过点![]() .点
.点![]() 在
在![]() 轴上,且
轴上,且![]() ,反比例函数图象上有一点
,反比例函数图象上有一点![]() ,且
,且![]() ,则点
,则点![]() 坐标为____.
坐标为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率; (用树形图或列表表示所有可能的结果)
(2)求三次传球后,球恰在A手中的概率. (用树形图或列表表示所有可能的结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
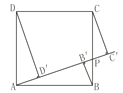
【题目】如图,正方形ABCD的边长为1,点P为BC上任意一点(可与点B或C重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最小值是( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com