
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率; (用树形图或列表表示所有可能的结果)
(2)求三次传球后,球恰在A手中的概率. (用树形图或列表表示所有可能的结果)
【答案】(1)![]() ,见解析;(2)
,见解析;(2)![]() ,见解析
,见解析
【解析】
(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次传球后,球恰在B手中的情况,再利用概率公式即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与三次传球后,球恰在A手中的情况,再利用概率公式即可求得答案.
(1)画树状图得:
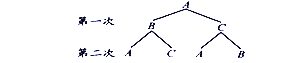
∵共有4种等可能的结果.(ABA、ABC、ACA、ACB),两次传球后,球恰在B手中的只有1种情况.
∴两次传球后,球恰在B手中的概率为![]()
(2)画树状图得:
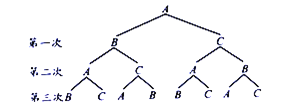
∵共有8种等可能的结果.(ABAB、ABAC、ABCA、ABCB、ACAB、ACAC、ACBA、ACBC).三次传球后,球恰在A手中的有2种情况.
∴三次传球后,球恰在A手中的概率为![]() .
.


科目:初中数学 来源: 题型:
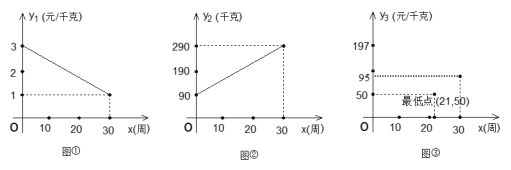
【题目】某水产基地种植某种食用海藻,从三月一日起的30周内,它的市场价格与上市时间的关系用图①线段表示;它的平均亩产量与时间的关系用图②线段表示;它的每亩平均成本与上市时间的关系用图③抛物线表示.
(1)写出图①、图②所表示的函数关系式;
(2)若市场价×亩产量-亩平均成本 = 每亩总利润,问哪一周上市的海藻利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
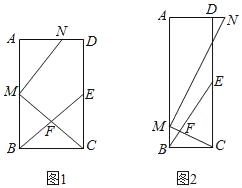
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连接CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)如图1,当点F为BE中点时,求证:AM=CE;
(2)如图2,若![]() =3时,求
=3时,求![]() 的值;
的值;
(3)若![]() =n(n≥3)时,请直接写出
=n(n≥3)时,请直接写出![]() 的值.(用含n的代数式表示)
的值.(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点,将线段
上一动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() ,连接
,连接![]() 并延长,分别交
并延长,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(1)如图1,若![]() 且
且![]() ,求菱形
,求菱形![]() 的面积;
的面积;
(2)如图2,求证:![]() .
.
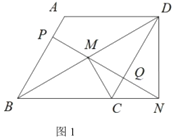
查看答案和解析>>
科目:初中数学 来源: 题型:
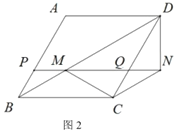
【题目】在△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC交AD于E,交AC于G,GF⊥BC于F,连接EF.
(1)如图1,求证:四边形AEFG是菱形;
(2)如图2,若E为BG的中点,过点E作EM∥BC交AC于M,在不添加任何辅助线的情况下,请直接写出图2中是CM长![]() 倍的所有线段.
倍的所有线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试比较图中两个几何图形的异同,请分别写出它们的两个相同点和两个不同点。例如,相同点:正方形的对角线相等,正五边形的。对角线也相等;不同点:正方形是中心对称图形,正五边形不是中心对称图形。
相同点:①_________________;②___________________
不同点:①______________________;②____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(-1,0);⑤当1<x<4时,有y2<y1,其中正确的是()
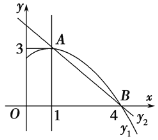
A.①④⑤B.①③④⑤C.①③⑤D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图.
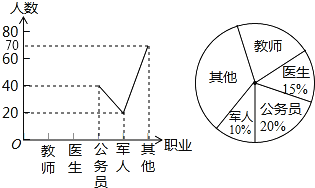
(1)把折线统计图补充完整;
(2)求出扇形统计图中,公务员部分对应的圆心角的度数;
(3)若从被调查的学生中任意抽取一名,求取出的这名学生最喜欢的职业是“教师”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com