
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点,将线段
上一动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() ,连接
,连接![]() 并延长,分别交
并延长,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
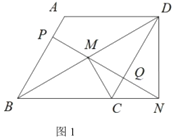
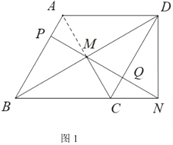
(1)如图1,若![]() 且
且![]() ,求菱形
,求菱形![]() 的面积;
的面积;
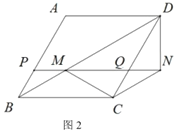
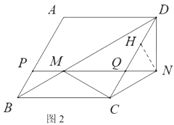
(2)如图2,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)连接![]() ,可得
,可得![]() ,进而得
,进而得![]() 、
、![]() 、
、![]() 三点共线,点M是菱形
三点共线,点M是菱形![]() 的旋转中心,可得
的旋转中心,可得![]() ,结合旋转的性质可得
,结合旋转的性质可得![]() ,MQ=NQ,根据直角三角形的性质得
,MQ=NQ,根据直角三角形的性质得![]() ,BM=4
,BM=4![]() ,进而即可求解;
,进而即可求解;
(2)根据菱形的性质和旋转的性质以及SAS,可证![]() ,在
,在![]() 上取点
上取点![]() ,使
,使![]() ,可证
,可证![]() ,再证
,再证![]() ,即可得到结论.
,即可得到结论.
(1)连接![]() ,如图1,
,如图1,
∵在菱形![]() 中,
中,![]() ,
,
又∵![]() ,
,
∴![]() 、
、![]() 、
、![]() 三点共线,点M是菱形
三点共线,点M是菱形![]() 的旋转中心,
的旋转中心,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵CM=CN,
∴![]() ,MQ=NQ,
,MQ=NQ,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵∠MBC=![]() ∠ABC=30°,
∠ABC=30°,
∴BM=4![]() ,
,
∴![]() 菱形
菱形![]() =32
=32![]() ;
;
(2)四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
由旋转的性质得:![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵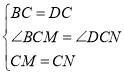 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 上取点
上取点![]() ,使
,使![]() ,如图2,
,如图2,
在![]() 和
和![]() 中,
中,
∵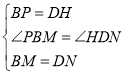 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴∠DHN=∠CQN,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】春天来了,我校计划组织师生共![]() 人坐
人坐![]() 、
、![]() 两种型号的大巴车外出春游,且
两种型号的大巴车外出春游,且![]() 型车每辆租金为
型车每辆租金为![]() 元,
元,![]() 型车每辆租金为
型车每辆租金为![]() 元,为了保证安全,校方要求必须保证人人都有座位.学生南南发现若租
元,为了保证安全,校方要求必须保证人人都有座位.学生南南发现若租![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车恰好能坐下
型大巴车恰好能坐下![]() 人,若租
人,若租![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车恰好能坐下
型大巴车恰好能坐下![]() 人.
人.
(1)请问![]() 辆
辆![]() 型与
型与![]() 辆
辆![]() 型大巴车各有几座?
型大巴车各有几座?
(2)现学校决定租两种型号的大巴车共![]() 辆作为出行交通工具,但政教主任蒋老师发现租车总经费不能超过
辆作为出行交通工具,但政教主任蒋老师发现租车总经费不能超过![]() 元.他想运用函数的知识进行分析,为学校寻找最节省的租车方案.现蒋老师设学校租了
元.他想运用函数的知识进行分析,为学校寻找最节省的租车方案.现蒋老师设学校租了![]() 型大巴车
型大巴车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.请你帮蒋老师完成分析过程,确定共有几种租车方案?哪种租车方案最省钱?并求出最低费用.
元.请你帮蒋老师完成分析过程,确定共有几种租车方案?哪种租车方案最省钱?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
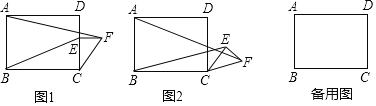
【题目】如图1,在矩形ABCD中,AB=6,BC=8,点E是边CD上的点,且CE=4,过点E作CD的垂线,并在垂线上截取EF=3,连接CF.将△CEF绕点C按顺时针方向旋转,记旋转角为a.
(1)问题发现
当a=0°时,AF= ,BE= ,![]() = ;
= ;
(2)拓展探究
试判断:当0°≤a°<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△CEF旋转至A,E,F三点共线时,直接写出线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级全体学生物理实验操作的情况,随机抽取了30名学生的物理实验操作考核成绩,并将数据进行整理,分析如下: (说明:考核成绩均取整数,A级:10分,B级:9分,C级:8分,D级:7分及以下)
收集数据
10,8,10,9,5,10,9,9,10,8,9,10,9,9,8,9,8,10,7,9,8,10,9,6,9,10,9,10,8,10
整理数据
整理、描述样本数据,绘制统计表如下:
抽取的30名学生物理实验操作考核成绩频数统计表
成绩等级 | A | B | C | D |
人数(名) | 10 | m | n | 3 |
根据表中的信息,解答下列问题:
(1)m=________,n=________;
(2)若该校九年级共有800名学生参加物理实验操作考核,成绩不低于9分为优秀,试估计该校九年级参加物理实验操作考核成绩达到优秀的学生有多少名?
(3)甲、乙、丙、丁是九年级1班物理实验考核成绩为10分的四名学生,学校计划从这四名学生中随机选出两名学生代表学校去参加全市中学生“物理实验操作”竞赛,用列表法或画树状图法,求甲、乙两名学生中至少有一名被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
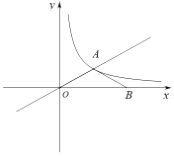
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,正比例函数
为坐标原点,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象都经过点
的图象都经过点![]() .点
.点![]() 在
在![]() 轴上,且
轴上,且![]() ,反比例函数图象上有一点
,反比例函数图象上有一点![]() ,且
,且![]() ,则点
,则点![]() 坐标为____.
坐标为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B、C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率; (用树形图或列表表示所有可能的结果)
(2)求三次传球后,球恰在A手中的概率. (用树形图或列表表示所有可能的结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
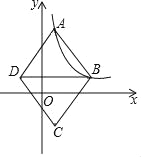
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y=![]() (k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为
(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,直线
,直线![]() 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线![]() 交于点
交于点![]() .
.
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若![]() 的面积为6,求直线CD的表达式.
的面积为6,求直线CD的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com