
(本题12分)如图,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,AC>CD,∠ACB=∠DCE且点A、D、E在同一直线上,连接BE.
(1)若∠ACB=60°, 则∠AEB的度数为 ;
线段AD、BE之间的数量关系是 .
(2)若∠ACB=∠DCE=90°, CM为△DCE中DE边上的高.
①求∠AEB的度数.
②若 ,
, ,试求CM的长.(请写全必要的证明和计算过程)
,试求CM的长.(请写全必要的证明和计算过程)

(1)60°,AD=BE;
(2)①∠AEB =90°,
②在CM= 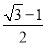
【解析】
试题分析:(1)∵∠ACB=∠DCE,∠CDB=∠CDB,
∴∠ACD=∠BCE
又∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS)
∴∠ADC=∠BEC,AD=BE
若∠ACB=60°,则△ABC和△CDE均为等边三角形,∠ADC=120°,从而∠BEC =120°,∠AEB =60°
故答案为:60°,AD=BE;
(2)①∵∠ACB=∠DCE,∠CDB=∠CDB,
∴∠ACD=∠BCE
又∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS)
∴∠ADC=∠BEC,AD=BE
若∠ACB=90°,则△ABC和△CDE均为等腰直角三角形,∠ADC=135°,从而∠BEC =135°,∠AEB =135°-45°=90°,
②在等腰直角△ABC中,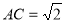 ,由勾股定理知:AB=2,
,由勾股定理知:AB=2,
在等腰直角△AEB中,因为BE=1, AB=2,由勾股定理知:AE=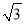 ,
,
又因为AD=BE=1,所以DE=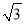 -1,
-1,
因为△CDE均为等腰直角三角形,CM为△DCE中DE边上的高,
所以CM= 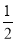 DE=
DE=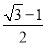
考点:1.等腰三角形的性质2.勾股定理3.三角形的全等的判定及性质


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源:2014-2015学年江苏省七年级上学期期中联考数学试卷(解析版) 题型:解答题
出租车司机小王某天下午营运全是在东西走向的太湖大道上进行的.如果向东记作“+”,向西记作“-”.他这天下午行车情况如下:(单位:千米)
-2,+5,-1,+10,-3,-2,-5,+6
请回答:
(1)小王将最后一名乘客送到目的地时,小王在下午出车的出发地的什么方向?距下午出车的出发地多远?
(2)若规定每趟车的起步价是10元,且每趟车3千米以内(含3千米)只收起步价;若超过3千米,除收起步价外,超过的每千米还需收2元钱.那么小王这天下午共收到多少钱?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市高新区九年级上学期期中联考数学试卷(解析版) 题型:选择题
如果关于 的方程
的方程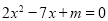 的两实数根互为倒数,那么
的两实数根互为倒数,那么 的值为( )
的值为( )
A. B.
B. C.2 D.
C.2 D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰州市姜堰区八年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题10分)如图,将在Rt△ABC绕其锐角顶点A旋转90°得到Rt△ADE,连接BE,延长DE、BC相交于点F,则有∠BFE=90°,且四边形ACFD是一个正方形.

(1)判断△ABE的形状,并证明你的结论;
(2)用含b的代数式表示四边形ABFE的面积;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市青阳片七年级上学期期中考试数学试卷 题型:选择题
甲从一个鱼摊买三条鱼,平均每条 元,又从另一个鱼摊买了两条鱼,平均每条
元,又从另一个鱼摊买了两条鱼,平均每条 元,后来他又以每条
元,后来他又以每条 元的价格把鱼全部卖给了乙,结果发现赔了钱,原因是 ( )
元的价格把鱼全部卖给了乙,结果发现赔了钱,原因是 ( )
A. B.
B.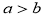 C.
C. D.与
D.与 和
和 大小无关
大小无关
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰州市海陵区九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分10分)按要求解下列一元二次方程:
(1) (配方法);
(配方法);
(2) (公式法).
(公式法).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市长泾片八年级上学期期中考试数学试卷(解析版) 题型:选择题
在联合会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A.三边中线的交点
B.三条角平分线的交点
C.三边中垂线的交点
D.三边上高的交点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com