
| A�� | ����x2-4x+3=0��3�������� | |
| B�� | ������x�ķ��̣�x-3����mx+n��=0��3�������̣���m+n=0 | |
| C�� | ��m+n=0��m��0�������x�ķ��̣�x-3����mx+n��=0��3�������� | |
| D�� | ��3m+n=0��m��0�������x�ķ���x2+��m-n��x-mn=0��3�������� |
���� ͨ����һԪ���̿ɶ�A�����жϣ��Ƚⷽ�̵õ�x1=3��x2=-$\frac{n}{m}$��Ȼ��ͨ���������۵õ�m��n�Ĺ�ϵ����ɶ�B�����жϣ��Ƚⷽ�̣�������m+n=0���ж������Ĺ�ϵ����ɶ�C�����жϣ��Ƚⷽ�̣�������3m+n=0���ж������Ĺ�ϵ����ɶ�D�����жϣ�
��� �⣺A���ⷽ��x2-4x+3=0��x1=1��x2=3������Aѡ���˵����ȷ��
B���ⷽ�̵�x1=3��x2=-$\frac{n}{m}$����-$\frac{n}{m}$=3��3����9m+n=0����-$\frac{n}{m}$=$\frac{1}{3}$��3����m+n=0������Bѡ���˵������
C���ⷽ�̵�x1=3��x2=-$\frac{n}{m}$����m+n=0����x2=1������Cѡ���˵����ȷ��
D���ⷽ�̵�x1=-m��x2=n����3m+n=0����n=-3m������x2=3x1������Dѡ���˵����ȷ��
��ѡB��
���� ���⿼���˸���ϵ���Ĺ�ϵ����x1��x2��һԪ���η���ax2+bx+c=0��a��0��������ʱ��x1+x2=$\frac{b}{a}$��x1x2=$\frac{c}{a}$��Ҳ������һԪ���η��̵Ľ�ͽ�һԪ���η��̣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{a}{b}$��3=$\frac{{a}^{3}}{b}$ | B�� | 3a3•2a2=6a6 | C�� | 4a6��2a2=2a3 | D�� | ��3a2��3=27a6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 5 | C�� | 3 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+a2=a4 | B�� | ��-a2��3=��-a��6 | C�� | [��-a��2]3=a6 | D�� | ��a2��3��a2=a3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
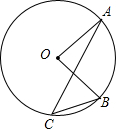 ��ͼ����O��A��B��C���㣬����B=50�㣬��A=20�㣬���AOB���ڣ�������
��ͼ����O��A��B��C���㣬����B=50�㣬��A=20�㣬���AOB���ڣ�������| A�� | 30�� | B�� | 50�� | C�� | 60�� | D�� | 70�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

| �˶�Ա | ƽ���� | ���� | ��λ�� | ���� |
| �� | 601.8 | 600 | 600 | 50.56 |
| �� | 599.3 | 618 | 595.5 | 284.21 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
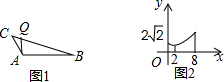 ��ͼ1���ڶ۽ǡ�ABC�У���Q�ӵ�C��ʼ�������B�˶������˶������У����߶�CQ�ij�Ϊx���߶�AQ�ij�Ϊy��y����x�ĺ���ͼ����ͼ2��ʾ��������Ϊ2ʱ���Ǻ���ͼ�����͵㣬������˵������ȷ���ǣ�������
��ͼ1���ڶ۽ǡ�ABC�У���Q�ӵ�C��ʼ�������B�˶������˶������У����߶�CQ�ij�Ϊx���߶�AQ�ij�Ϊy��y����x�ĺ���ͼ����ͼ2��ʾ��������Ϊ2ʱ���Ǻ���ͼ�����͵㣬������˵������ȷ���ǣ�������| A�� | ��C�Ķ���Ϊ45�� | B�� | AQ����СֵΪ2 | C�� | ��ABC�����Ϊ8 | D�� | sinB��ֵΪ$\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com