
直线 与
与 轴交于点C(4,0),与
轴交于点C(4,0),与 轴交于点B,并与双曲线
轴交于点B,并与双曲线
 交于点
交于点 。
。
(1)求直线与双曲线的解析式。
(2)连接OA,求 的正弦值。
的正弦值。
(3)若点D在 轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。
轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。

(1) y=x-4;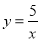 ;(2)
;(2) 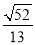 ;(3) (6,0)或(20,0).
;(3) (6,0)或(20,0).
【解析】
试题分析:(1)把点C的坐标代入y=x+b,求出b的值,得出直线的解析式;把点A(-1,n)代入y=x-4得到n的值,求出A点的坐标,再把将A点代入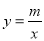 (x<0)中,求出m的值,从而得出双曲线的解析式;
(x<0)中,求出m的值,从而得出双曲线的解析式;
(2)先过点O作OM⊥AC于点M,根据B点经过y轴,求出B点的坐标,根据勾股定理求出AO的值,根据OC=OB=4,得出△OCB是等腰三角形,求出∠OBC=∠OCB的度数,再在△OMB中,根据正弦定理求出OM的值,从而得出∠OAB的正弦值.
(3)先过点A作AN⊥y轴,垂足为点N,根据AN=1,BN=1,求出AB的值,根据OB=OC=4,求出BC的值,再根据∠OBC=∠OCB=45°,得出∠OBA=∠BCD,从而得出△OBA∽△BCD或△OBA∽△DCB,最后根据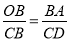 ,再代入求出CD的长,即可得出答案.
,再代入求出CD的长,即可得出答案.
试题解析:(1)∵直线y=x+b与x轴交于点C(4,0),
∴把点C(4,0)代入y=x+b得:b=-4,
∴直线的解析式是:y=x-4;
∵直线也过A点,
∴把A点代入y=x-4得到:n=-5
∴A(-1,-5),
把将A点代入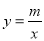 (x<0)得:m=5,
(x<0)得:m=5,
∴双曲线的解析式是: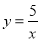 ;
;
(2)过点O作OM⊥AC于点M,
∵B点经过y轴,
∴x=0,
∴0-4=y,
∴y=-4,
∴B(0,-4),
AO=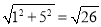 ,
,
∵OC=OB=4,
∴△OCB是等腰三角形,
∴∠OBC=∠OCB=45°,
∴在△OMB中 sin45°=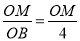 ,
,
∴OM=2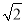 ,
,
∴在△AOM中,
sin∠OAB=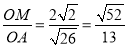 ;
;
(3)存在;
过点A作AN⊥y轴,垂足为点N,
则AN=1,BN=1,
则AB=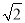 ,
,
∵OB=OC=4,
∴BC=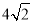 ,
,
∠OBC=∠OCB=45°,
∴∠OBA=∠BCD=135°,
∴△OBA∽△BCD或△OBA∽△DCB,
∴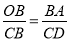 ,
,
∴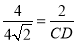 或
或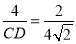 ,
,
∴CD=2或CD=16,
∴点D的坐标是(6,0)或(20,0).
考点:反比例函数综合题.


科目:初中数学 来源:2013-2014学年山东省淄博市桓台县九年级中考模拟数学试卷(解析版) 题型:选择题
如图,在△ABC中,AD是高,△ABC的外接圆直径AE交BC边于点G,有下列四个结论:①AD2=BD•CD;②BE2=EG•AE;③AE•AD=AB•AC;④AG•EG=BG•CG.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市九年级中考模拟数学试卷(解析版) 题型:解答题
如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长;
(3)填空:在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市九年级中考模拟数学试卷(解析版) 题型:选择题
如图,已知等腰梯形ABCD的底角∠B=45°,高AE=1,上底AD=1,则其面积为( )
A.4 B. C.1 D.2
C.1 D.2

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:填空题
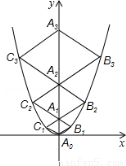
二次函数y= 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
=60°,菱形An﹣1BnAnCn的周长为 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:选择题
如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s( ),则s(
),则s( )与t(s)的函数关系可用图像表示为( )
)与t(s)的函数关系可用图像表示为( )


查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:解答题
已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连结BD.
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省德州市九年级第一次模拟考试数学试卷(解析版) 题型:选择题
如图a是长方形纸带,∠DEF=25°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠DHF的度数是

A.35° B.50° C.65° D.75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com