
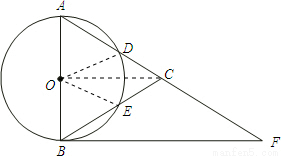
如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长;
(3)填空:在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为 .

(1)证明见解析;(2)BF=10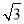 ;(3)5
;(3)5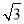 ?5<r<5+5.
?5<r<5+5.
【解析】
试题分析:(1)欲证明直线BF是⊙O的切线,只需证明AB⊥BF;
(2)根据圆心角、弧、弦间的关系,等边三角形的判定证得△AOD是等边三角形,所以在Rt△ABF中,∠ABF=90°,∠OAD=60°,AB=10,则利于∠A的正切三角函数的定义来求BF边的长度;
(3)根据已知条件知⊙O与⊙C相交.
(1)证明:如图,∵∠CBF=∠CFB,
∴CB=CF.
又∵AC=CF,
∴CB=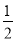 AF,
AF,
∴△ABF是直角三角形,
∴∠ABF=90°,即AB⊥BF.
又∵AB是直径,
∴直线BF是⊙O的切线.
(2)【解析】
如图,连接DO,EO,
∵点D,点E分别是弧AB的三等分点,
∴∠AOD=60°.
又∵OA=OD,
∴△AOD是等边三角形,
∴OA=AD=OD=5,∠OAD=60°,
∴AB=10.
∴在Rt△ABF中,∠ABF=90°,BF=AB•tan60°=10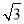 ,即BF=10
,即BF=10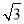 ;
;
(3)如图,连接OC.则OC是Rt△ABF的中位线,
∵由(2)知,BF=10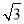 ,
,
∴圆心距OC=5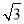 ,
,
∵⊙O半径OA=5.
∴5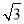 ?5<r<5
?5<r<5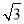 +5.
+5.
故填:5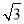 ?5<r<5+5.
?5<r<5+5.
考点:圆的综合题.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源:2013-2014学年山东省初中学业水平考试数学模拟试卷(解析版) 题型:填空题
如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数 的图象经过点C,则k的值为 .
的图象经过点C,则k的值为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,直线 =
= 分别与
分别与 轴,
轴, 轴相交于
轴相交于 两点,点
两点,点 是
是 轴的负半轴上的一个动点,以
轴的负半轴上的一个动点,以 为圆心,3为半径作
为圆心,3为半径作 .
.
(1)连结 ,若
,若 ,试判断
,试判断 与
与 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(2)当 为何值时,以
为何值时,以 与直线
与直线 =
= 的两个交点和圆心
的两个交点和圆心 为顶点的三角形是正三角形?
为顶点的三角形是正三角形?

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:选择题
如图,在□ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于
A.1.5cm B.2cm C.2.5cm D.3cm

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市长清区九年级复习调查考试(一模)数学试卷(解析版) 题型:选择题
下列多项式中,能用公式法分解因式的是
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省济南市九年级中考模拟数学试卷(解析版) 题型:选择题
如图,直线l:y=-x- 与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合),
与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合), 的值是否发生变化?( )
的值是否发生变化?( )
A. B.
B. C.2 D.变化
C.2 D.变化

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省九年级第一次学业水平模拟考试数学试卷(解析版) 题型:解答题
直线 与
与 轴交于点C(4,0),与
轴交于点C(4,0),与 轴交于点B,并与双曲线
轴交于点B,并与双曲线
 交于点
交于点 。
。
(1)求直线与双曲线的解析式。
(2)连接OA,求 的正弦值。
的正弦值。
(3)若点D在 轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。
轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在求出D点的坐标,若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东省泰安市九年级学业模拟考试数学试卷(解析版) 题型:选择题
二次函数y=(2x-1)2+2的顶点的坐标是
A.(1,2) B.(1,-2) C.( ,2) D.(-
,2) D.(- ,-2)
,-2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com