
【题目】如图,将一段12cm长的管道竖直置于地面,并在上面放置一个半径为5cm的小球,放置完毕以后小球顶端距离地面20cm,则该管道的直径AB为 . 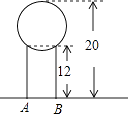
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,明亮同学在点A处测得大树顶端C的仰角为36°,斜坡AB的坡角为30°,沿在同一剖面的斜坡AB行走16米至坡顶B处,然后再沿水平方向行走6.4米至大树脚底点D处,那么大树CD的高度约为多少米?)(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73, ![]() ≈1.7).
≈1.7).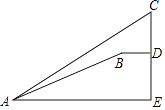
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,BC=6,AD=3,∠DCB=30°.点E、F同时从B点出发,沿射线BC向右匀速移动,已知F点移动速度是E点移动速度的2倍,以EF为一边在CB的上方作等边△EFG,设E点移动距离为x(x>0).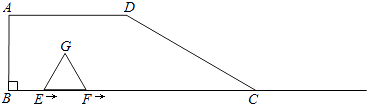
(1)△EFG的边长是(用含有x的代数式表示),当x=2时,点G的位置在;
(2)若△EFG与梯形ABCD重叠部分面积是y,求y与x之间的函数关系式;
(3)探究(2)中得到的函数y在x取何值时,存在最大值?并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的面积是60,请完成下列问题:
(1)如图①,若AD是△ABC的BC边上的中线,则△ABD的面积 _△ACD的面积(选填“>”“<”或“=”).
(2)如图②,若CD,BE分别是△ABC的AB,AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y,由题意得:S△ABE=![]() S△ABC=30,S△ADC=
S△ABC=30,S△ADC=![]() S△ABC=30,可列方程组为: ,通过解这个方程组可得四边形ADOE的面积为 .
S△ABC=30,可列方程组为: ,通过解这个方程组可得四边形ADOE的面积为 .
(3)如图③,AD∶DB=1∶3,CE∶AE=1∶2,请你计算四边形ADOE的面积,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明,小红等同学随父母一同去某景点旅游,在购买门票时,小明和小红有图1所示的对话,根据图2的门票票价和图1所示的对话内容完成下列问题.
(1)他们一共去了几个成人几个学生?
(2)请你帮他们算一算,用哪种方式买票更省钱,省多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种新运算“⊕”:a⊕b=2a﹣ab,比如1⊕(﹣3)=2×1﹣1×(﹣3)=5
(1)求(﹣2)⊕3的值;
(2)若(﹣3)⊕x=(x+1)⊕5,求x的值;
(3)若x⊕1=2(1⊕y),求代数式![]() x+y+1的值.
x+y+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
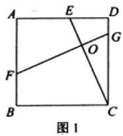
【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,则OE的长为_________(直接写出结果).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com