练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在ABCD中，点E在BC边上，且AE⊥BC于点E，DE平分∠CDA.若BE∶EC＝1∶2，则∠BCD的度数为________．

    【答案】120°

    【解析】由平行四边形的性质和已知条件得出∠CED=∠CDE，证出CD=EC=AB，得出BE=AB，再在Rt△ABE中求出∠BAE，得出∠B，即可求出∠BCD的度数．

    ∵四边形ABCD是平行四边形，∴AB=CD，AD∥BC，AB∥CD，

    ∴∠ADE=∠CED，∠B+∠BCD=180°．

    ∵ED平分∠CDA，∴∠ADE=∠CDE，

    ∴∠CED=∠CDE，∴CD=EC，∴AB=EC．

    ∵BE：EC=1：2，∴BE：AB=1：2，即BE=AB．

    ∵AE⊥BC，∴∠AEB=90°，∴∠BAE=30°，

    ∴∠B=60°，∴∠BCD=120°．

    故答案为：120°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】列一元一次方程解应用题：

    社会是一个重要的学校和课堂，生活是一种重要的课程和教材，实践是一种重要的学习方式和途径．参加社会生活和社会实践，不仅可以学到很多在课堂上学不到的东西，也可以把课堂上学到的理论知识同社会实践联系起来，加深对课堂学习内容的理解，我区某校七年级学生在农场进行社会实践活动时，采摘了黄瓜和茄子共80千克，了解到这些蔬菜的种植成本共180元，还了解到如下信息：

    （1）求采摘的黄瓜和茄子各多少千克？

    （2）这些采摘的黄瓜和茄子可赚多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点.

    请解决下列问题：

    （1）已知点M，N是线段AB的勾股分割点，且BN>MN>AM.若AM=2，MN=3，求BN的长；

    （2）如图2，若点F、M、N、G分别是AB、AD、AE、AC边上的中点，点D，E是线段BC的勾股分割点，且EC>DE>BD，求证：点M，N是线段FG的勾股分割点.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    （1）（）×（﹣30）

    （2）﹣22×|﹣3|+（﹣6）2×（﹣）﹣÷（﹣）3

    （3）5（a2b﹣3ab2）﹣2（a2b﹣7ab2）

    （4）a2b﹣0.4ab2﹣a2b+ab2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

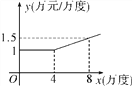
    【题目】某工厂在生产过程中每消耗1万度电可以产生产值5.5万元，电力公司规定，该工厂每月用电量不得超过16万度；月用电量不超过4万度时，单价都是1万元/万度；超过4万度时，超过部分电量单价将按用电量进行调整．电价y与月用电量x的函数关系可以用下图来表示(效益＝产值－用电量×电价)．

    (1)求y与月用电量x之间的函数关系式，并写出自变量的取值范围；

    (2)设工厂的月效益为z(万元)，写出z与用电量x之间的函数关系式；

    (3)求工厂最大月效益．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一数值转换器，原理如图所示，若开始输入x的值是7，可发现第1次输出的结果是12；第2次输出的结果是6；依次继续下去……第2018次输出的结果是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了能有效地使用电力资源，镇江市市区实行居民峰谷用电，居民家庭在峰时段（上午8:00～晚上21:00）用电的电价为0.55元/千瓦时，谷时段（晚上21:00～次日晨8:00）用电的电价为0.35元/千瓦时．若某居民户某月用电100千瓦时，其中峰时段用电x千瓦时．

    （1）请用含x的代数式表示该居民户这个月应缴纳电费；

    （2）利用上述代数式计算，当x=40时，求应缴纳电费；

    （3）若缴纳电费为50元，求谷时段用电多少千瓦时．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一段12cm长的管道竖直置于地面，并在上面放置一个半径为5cm的小球，放置完毕以后小球顶端距离地面20cm，则该管道的直径AB为 ．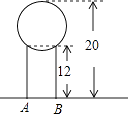

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB是⊙O的直径，点C、D在⊙O上，∠D=60°且AB=6，过O点作OE⊥AC，垂足为E．

    （1）求OE的长；
    （2）若OE的延长线交⊙O于点F，求弦AF、AC和弧CF围成的图形（阴影部分）的面积S．

    查看答案和解析>>

    同步练习册答案