
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,且点
两点,且点![]() 的横坐标和点
的横坐标和点![]() 的纵坐标都是
的纵坐标都是![]() ,求:
,求:

![]() 一次函数的解析式;(2)
一次函数的解析式;(2)![]() 的面积.
的面积.
![]() 根据图象回答:当
根据图象回答:当![]() 为何值时,一次函数的函数值大于反比例函数的函数值.
为何值时,一次函数的函数值大于反比例函数的函数值.
【答案】(1)![]() ;(2)6;(3)
;(2)6;(3)![]() 或
或![]() .
.
【解析】
1、由已知点可求得A,B的坐标,带入一次函数解析式即可求得一次函数解析式.
2、由一次函数解析式可以求得N点坐标,然后可以运用S=ON×(A的横坐标+B的横坐标),即可得出答案.
3、当一次函数图像在反比例函数图像上方时,一次函数的函数值大于反比例函数的函数值.
解:![]() 令反比例函数
令反比例函数![]() 中
中![]() ,则
,则![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
反比例函数![]() 中
中![]() ,则
,则![]() ,
,
解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵一次函数过![]() 、
、![]() 两点,
两点,
∴![]() ,解得:
,解得:![]() ,
,
∴一次函数的解析式为![]() .
.
![]() 令为
令为![]() 中
中![]() ,则
,则![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() .
.
![]() 观察函数图象发现:
观察函数图象发现:
当![]() 或
或![]() 时,一次函数图象在反比例函数图象上方,
时,一次函数图象在反比例函数图象上方,
∴一次函数的函数值大于反比例函数的函数值时![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用下图的三角形解释二项和的乘方规律.杨辉在注释中提到,在他之前北宋数学家贾宪(1050年左右)也用过上述方法,因此我们称这个三角形为“杨辉三角”或“贾宪三角”.杨辉三角两腰上的数都是![]() ,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了
,其余每一个数为它上方(左右)两数的和.事实上,这个三角形给出了![]()
![]() 的展开式(按
的展开式(按![]() 的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的
的次数由大到小的顺序)的系数规律.例如,此三角形中第三行的![]() 个数
个数![]() ,恰好对应着
,恰好对应着![]() 展开式中的各项系数,第四行的
展开式中的各项系数,第四行的![]() 个数
个数![]() ,恰好对应着
,恰好对应着![]() 展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题:
展开式中的各项系数,等等.请依据上面介绍的数学知识,解决下列问题:
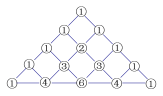
(1)写出![]() 的展开式;
的展开式;
(2)利用整式的乘法验证你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BF和CE分别是钝角△ABC(∠ABC是钝角)中AC、AB边上的中线,又BF⊥CE,垂足是G,过点G作GH⊥BC,垂足为H.
(1)求证:GH2=BHCH;
(2)若BC=20,并且点G到BC的距离是6,则AB的长为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)sin45°cos60°﹣cos45°sin30°;
(2)5tan30°﹣2(cos60°﹣sin60°);
(3)(![]() tan30°)2005(2
tan30°)2005(2![]() sin45°)2004;
sin45°)2004;
(4)![]() (2cos45°﹣tan45°)﹣(tan60°+sin30°)0﹣(2sin45°﹣1)﹣1.
(2cos45°﹣tan45°)﹣(tan60°+sin30°)0﹣(2sin45°﹣1)﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=![]() BC=1,则下列结论:
BC=1,则下列结论:
①∠CAD=30°②BD=![]() ③S平行四边形ABCD=ABAC④OE=
③S平行四边形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正确的个数是( )
,正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
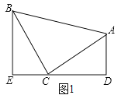
【题目】(1)(模型建立)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED与D,过B作BE⊥ED于E,求证:△BEC≌△CDA;
(2)(模型应用):已知直线![]() 与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;
与y轴交于A点,与x轴交于B点,将线段AB绕点B逆时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”
请解答上述问题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com