
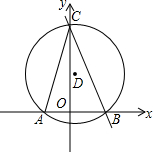
 已知,如图,在平面直角坐标系中,A(-2,0),B(3,0),直线l:y=kx+b经过B点,与y轴的正半轴交于C点,连接AC.此时∠ACB=45°,有一⊙D经过△ABC的三个顶点.
已知,如图,在平面直角坐标系中,A(-2,0),B(3,0),直线l:y=kx+b经过B点,与y轴的正半轴交于C点,连接AC.此时∠ACB=45°,有一⊙D经过△ABC的三个顶点.分析 (1)连接DA、DB,过点D作DH⊥x轴于H,如图,根据圆周角定理可得∠ADB=90°,运用勾股定理可求出⊙D的半径,然后运用等腰三角形的性质可求出BH,从而求出OH,再运用勾股定理求出DH,就可得到圆心D的坐标;
(2)点B的坐标已知,要求直线l解析式,只需求出点C的坐标,过点D作DG⊥OC于G,连接DC,易证四边形DGOH是矩形,从而可求出DG、OG,只需在Rt△DGC中运用勾股定理求出CG即可;
(3)只需运用勾股定理求出AC长,然后运用直角三角形的内切圆的半径公式,就可解决问题.
解答 解:(1)连接DA、DB,过点D作DH⊥x轴于H,如图,
∵A(-2,0),B(3,0),
∴OA=2,OB=3,AB=5.
∵∠ACB=45°,
∴∠ADB=2∠ACB=90°.
∴DA2+DB2=2DB2=AB2=25,
∴DB=$\frac{5\sqrt{2}}{2}$.
∵DA=DB,DH⊥AB,
∴AH=BH=$\frac{1}{2}$AB=$\frac{5}{2}$,
∴OH=3-$\frac{5}{2}$=$\frac{1}{2}$,DH=$\sqrt{D{B}^{2}-B{H}^{2}}$=$\frac{5}{2}$,
∴点D的坐标为($\frac{1}{2}$,$\frac{5}{2}$);
(2)过点D作DG⊥OC于G,连接DC,如图,
则有∠DGO=∠GOH=∠OHD=90°,
∴四边形DGOH是矩形,
∴DG=OH=$\frac{1}{2}$,OG=DH=$\frac{5}{2}$.
又∵DC=DB=$\frac{5\sqrt{2}}{2}$,
∴CG=$\sqrt{D{C}^{2}-D{G}^{2}}$=$\sqrt{\frac{50}{4}-\frac{1}{4}}$=$\frac{7}{2}$,
∴OC=OG+CG=$\frac{5}{2}$+$\frac{7}{2}$=6,
∴点C的坐标为(0,6).
∵点B(3,0)、C(0,6)在直线y=kx+b上,
∴$\left\{\begin{array}{l}{3k+b=0}\\{b=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$,
∴直线l的解析式为y=-2x+6;
(3)在Rt△AOC中,
∵OA=2,OC=6,
∴AC=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$,
∴Rt△AOC的内切圆的半径长为$\frac{OA+OC-AC}{2}$=$\frac{2+6-2\sqrt{10}}{2}$=4-$\sqrt{10}$.
点评 本题主要考查了运用待定系数法求直线的解析式、等腰三角形的性质、圆周角定理、矩形的判定与性质、勾股定理、直角三角形内切圆半径公式(r=$\frac{a+b-c}{2}$,c为斜边)等知识,在Rt△DGC中运用勾股定理求出CG是解决第(2)小题的关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源:2017届江西省高安市九年级下学期第一次模拟考试数学试卷(解析版) 题型:判断题
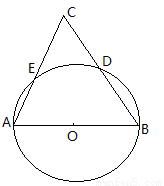
如图,以AB为直径的⊙O交△ABC的BC、AC边与D、E两点,在图中仅以没有刻度的直尺画出三角形的三条高(简单叙述你的画法)
查看答案和解析>>
科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:判断题
如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;……设游戏者从圈A起跳.

(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
(2)淇淇随机掷两次骰子,求最后落回到圈A的概率P2,并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:单选题
下列命题错误的是( )
A. 对角线互相垂直平分的四边形是菱形 B. 平行四边形的对角线互相平分
C. 矩形的对角线相等 D. 对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.
如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com