练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．已知△ABC与△A′B′C′关于点O成位似图形，相似比是2：5，OA=10，则OA′的长是25．

    分析 根据位似图形是相似图形，位似比即对应边的比计算即可．

    解答 解：∵△ABC与△A′B′C′关于点O成位似图形，
    ∴△ABC∽△A′B′C′，
    ∵相似比是2：5，
    ∴$\frac{OA}{OA′}$=$\frac{2}{5}$，
    又∵OA=10，
    ∴OA′=25，
    故答案为：25．

    点评 本题考查的是位似变换的定义，如果两个图形不仅是相似图形，而且对应顶点的连线相交于一点，对应边互相平行，那么这样的两个图形叫做位似图形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年浙江省杭州市萧山区戴村片八年级3月月考数学试卷（解析版） 题型：单选题

    某市2014年的快递业务量为4.4亿件，受益于电子商务发展和法治环境改善等多重因素，快递业务迅猛发展．若2016年的快递业务量达到9.7亿件，设2015年与2016年这两年的平均增长率为x，则下列方程正确的是()

    A. B.

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

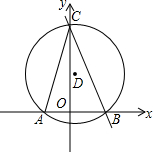    9．已知，如图，在平面直角坐标系中，A（-2，0），B（3，0），直线l：y=kx+b经过B点，与y轴的正半轴交于C点，连接AC．此时∠ACB=45°，有一⊙D经过△ABC的三个顶点．
    （1）求⊙D的圆心D的坐标；
    （2）求直线l解析式；
    （3）直接写出直角△AOC的内切圆的半径的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．己知：在四边形ABCD中，G、H分别是AD、BC的中点，AE⊥BD，CF⊥BD，垂足分别为E、F．
    （1）如图1，若四边形ABCD为平行四边形，求证：四边形GEHF是平行四边形．
    （2）如图2，若四边形ABCD为矩形，设$\frac{AD}{AB}$=n．请你给出一个n的值，使四边形GEHF为矩形，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．关于x的多项式乘多项式（x2-3x-2）（ax+1），若结果中不含有x的一次项，求代数式：2a（2a+1）-（2a+1）（2a-1）+1的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．问题情境：矩形ABCD中，∠ACB=30°，将一块直角三角板的直角顶点P放在两对角线的交点处，以点P为旋转中心转动三角板，并保证三角板的两直角边分别与边AB、BC所在的直线相交，交点为E、F．

    探究1：如图1，当PE⊥AB，PF⊥BC时，则$\frac{PE}{PF}$=$\sqrt{3}$；
    探究2：如图2，在（1）的基础上，将三角板绕点P逆时针旋转，旋转角为α，（0°＜α＜60°），试求$\frac{PE}{PF}$的值．
    探究3：在（2）的基础上继续旋转，当60°＜α＜90°时，将顶点P在AC上移动且使$\frac{AP}{PC}$=$\frac{1}{2}$时，如图3，试求$\frac{PE}{PF}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，平行四边形ABCD中，E是CD的中点，△ABE是等边三角形．求证：四边形ABCD是矩形．

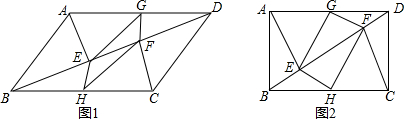
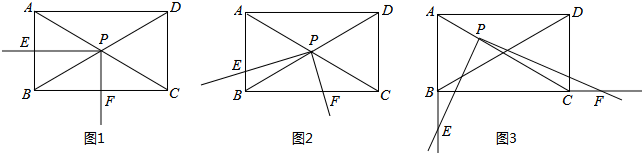
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．在平面内，先将一个多边形以点O为位似中心放大或缩小，使得新多边形与原多边形对应线段的比为k，并且原多边形上的任意一点P的对应点P1在线段OP或其延长线上：接着将所得多边形以O为旋转中心，逆时针旋转一个角度θ，这种经过放缩和旋转的图形变换叫做旋转相似变换，记为O（k，θ），其中O叫做旋转相似中心，k叫做相似比，θ叫做旋转角．现将直角边长为1的等腰直角三角形ABC（∠C=90°）作旋相似变换B（2，60°），若点A的对应点为D，则线段AD的长为$\sqrt{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知如图，?ABCD的对角线AC与BD相交于点O，OA、OB、AB的长分别是3，4，5．求其他各边以及两条对角线的长度．

    查看答案和解析>>

    同步练习册答案