
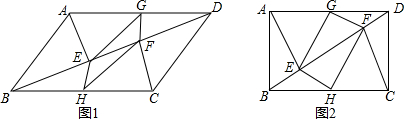
分析 (1)根据直角三角形斜边中线定理只要证明EG=HF,EG∥FH即可.
(2)结论n=$\sqrt{3}$,如图2中,连接GH,交BD于O,连接AO,先证明△ABO是等边三角形,再证明AB=EF,GH=AB,得EF=HG,即可证明.
解答 (1)证明:如图1中,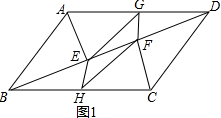 ∵AE⊥BD,CF⊥BD,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
∵AG=GD,BH=CH,
∴EG=$\frac{1}{2}$AD,HF=$\frac{1}{2}$BC,
∴∠GDE=∠GED,∠HBF=∠HFB,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠GDE=∠HBF,
∴EG=FH,∠GEF=∠HFE,
∴EG∥HF,
∴四边形GEHF是平行四边形.
(2)当n=$\sqrt{3}$时,四边形GEHF为矩形.
证明:如图2中,连接GH,交BD于O,连接AO.
由(1)可知,四边形GEHF是平行四边形,
∴OE=OF,
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵tan∠ABD=$\frac{AD}{AB}$=$\sqrt{3}$,
∴∠ABD=60°,∠ADB=30°,
∵AE⊥BD,
∴∠AED=90°,∠EAD=60°,∠BAE=30°,
∴BE=$\frac{1}{2}$AB,同理DF=$\frac{1}{2}$CD,
∵AB=CD,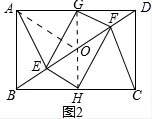
∴BE=DF,BO=OD,
∴AO=BO=DO,
∵∠ABD=60°,
∴△ABO是等边三角形,
∴AB=AO,∵AE⊥BO,
∴BE=EO,
∴EF=2BE=AB,
∵AG∥BH,AG=BH,
∴四边形ABHG是平行四边形,
∴AB=GH=EF,∵四边形GEHF是平行四边形,
∴四边形GEHF是矩形.
点评 本题考查平行四边形的判定和性质、矩形的判定和性质、直角三角形斜边中线定理、等边三角形的判定等知识,灵活运用这些知识是解决问题的关键,属于中考常考题型.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源:2016-2017学年浙江省杭州市萧山区戴村片八年级3月月考数学试卷(解析版) 题型:解答题
已知关于x的两个一元二次方程,
方程①: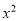
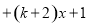 =0,
=0,
方程②: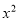

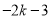 =0.
=0.
(1)若这两个方程中只有一个有实数根,请说明哪个方程没有实数根;
(2)如果这两个方程有一个公共根a,求代数式 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:单选题
下列命题错误的是( )
A. 对角线互相垂直平分的四边形是菱形 B. 平行四边形的对角线互相平分
C. 矩形的对角线相等 D. 对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com