
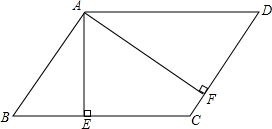
 如图.在平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F.该图中与∠EAF相等的有∠B、∠D.
如图.在平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F.该图中与∠EAF相等的有∠B、∠D.  通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:填空题
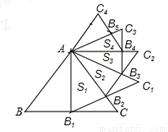
如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,那么S3 = ______,则Sn=______.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
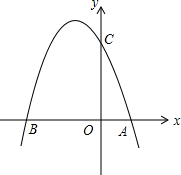 如图,抛物线y=-x2-2x+3与y轴交于点C,与x轴交于点A、B(点B在点A的左侧),设J为y轴正半轴上的一个点,请在抛物线y=-x2-2x+3上求一点K,使得△OKJ为等腰直角三角形.
如图,抛物线y=-x2-2x+3与y轴交于点C,与x轴交于点A、B(点B在点A的左侧),设J为y轴正半轴上的一个点,请在抛物线y=-x2-2x+3上求一点K,使得△OKJ为等腰直角三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com