
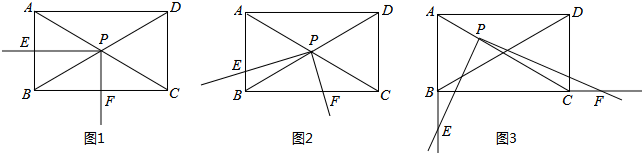
分析 (1)证明△APE≌△PCF,得PE=CF;在Rt△PCF中,解直角三角形求得$\frac{PE}{PF}$的值;
(2)如答图1所示,作辅助线,构造直角三角形,证明△PME∽△PNF,并利用(1)的结论,求得$\frac{PE}{PF}$的值;
(3)如答图2所示,作辅助线,构造直角三角形,首先证明△APM∽△PCN,求得$\frac{PM}{PN}$的值;然后证明△PME∽△PNF,从而由$\frac{PE}{PF}$求得$\frac{PE}{PF}$的值.与(1)(2)问相比较,$\frac{PE}{PF}$的值发生了变化.
解答 解:(1)∵矩形ABCD,
∴AB⊥BC,PA=PC;
∵PE⊥AB,BC⊥AB,
∴PE∥BC,
∴∠APE=∠PCF;
∵PF⊥BC,AB⊥BC,
∴PF∥AB,
∴∠PAE=∠CPF.
∵在△APE与△PCF中,
$\left\{\begin{array}{l}{∠PAE=∠CPF}\\{PA=PC}\\{∠APE=∠PCF}\end{array}\right.$,
∴△APE≌△PCF(ASA),
∴PE=CF.
在Rt△PCF中,$\frac{PF}{CF}$=tan30°=$\frac{\sqrt{3}}{3}$,
∴$\frac{PE}{PF}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
(2)如答图1,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN.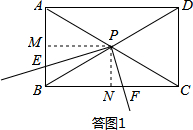
0°~30°时
∵PM⊥PN,PE⊥PF,
∴∠EPM=∠FPN,
又∵∠PME=∠PNF=90°,
∴△PME∽△PNF,
∴$\frac{PE}{PF}=\frac{PM}{PN}$,
由(1)知,$\frac{PM}{PN}=\sqrt{3}$,
∴$\frac{PE}{PF}=\sqrt{3}$.
同理30°~60°时,
$\frac{PE}{PF}=\frac{\sqrt{3}}{3}$;
(3)如答图2,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN,PM∥BC,PN∥AB.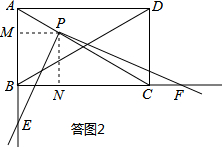
∵PM∥BC,PN∥AB,
∴∠APM=∠PCN,∠PAM=∠CPN,
∴△APM∽△PCN,
∴$\frac{PM}{CN}=\frac{AP}{PC}=\frac{1}{2}$,得CN=2PM.
在Rt△PCN中,$\frac{PN}{CN}$=$\frac{PN}{2PM}$=tan30°=$\frac{\sqrt{3}}{3}$,
∴$\frac{PM}{PN}=\frac{\sqrt{3}}{2}$.
∵PM⊥PN,PE⊥PF,
∴∠EPM=∠FPN,
又∵∠PME=∠PNF=90°,
∴△PME∽△PNF,
∴$\frac{PE}{PF}=\frac{PM}{PN}=\frac{\sqrt{3}}{2}$.
点评 本题是几何综合题,考查了相似三角形的判定与性质、矩形的性质、全等三角形的判定与性质、解直角三角形等知识点.本题三问的解题思路是一致的:即都是直接或作辅助线构造直角三角形,通过相似三角形或全等三角形解决问题.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
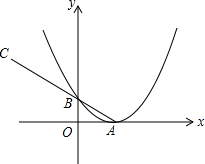 如图,抛物线y=$\frac{1}{4}$x2-x+1的顶点A在x轴上,与y轴交于B,延长AB至C,使BC=2AB,将抛物线向左平移n个单位,使抛物线与线段AC总有两个交点,求n的取值范围.
如图,抛物线y=$\frac{1}{4}$x2-x+1的顶点A在x轴上,与y轴交于B,延长AB至C,使BC=2AB,将抛物线向左平移n个单位,使抛物线与线段AC总有两个交点,求n的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com