
���� ��1�����������ε������жϳ�PC+PE����Сֵ��λ�ã�Ȼ���ļ��㣬���ɣ�
��2���������ε������жϳ�PB+PE����Сֵ��λ�ã�Ȼ���ļ��㣬���ɣ�
��3�����õ㵽ֱ�ߵľ����У����߶���̣�Ȼ����мļ��㼴�ɣ�
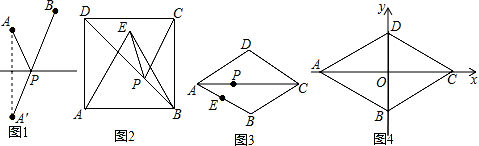
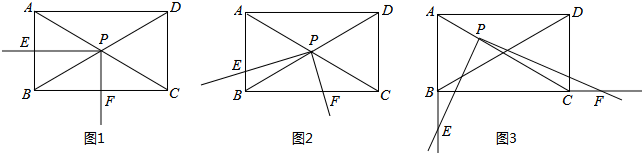
��� �⣺��1����ͼ1��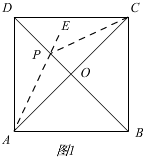
���������ε����ʿ�֪��
��C����BD�ĶԳƵ�Ϊ��A��
��PC+PE�ĺ���СֵΪAE��
��������ABCD�����Ϊ16��
��AB=4��
�ߡ�ABE�ǵȱ������Σ�
��AE=4��
��PC+PE�ĺ���СֵΪ4��
�ʴ�Ϊ4��
��2����ͼ2
�������ε����ʿ�֪��
��B����AC�ĶԳƵ�Ϊ��D��
��DEΪPB+PE����Сֵ��
�ߡ�B=120�㣬
���BAD=60�㣬
���ABD�ǵȱ������Σ�
��E��AB���е㣬����DE��AB��
��AB=2����AE=$\sqrt{3}$��
��PB+PE����Сֵ��$\sqrt{3}$��
�ʴ�Ϊ$\sqrt{3}$
��3��ʹ��P������̵�ʱ���ڵ����B����
�൱PB��ABʱ���������⣬
�ߡ�DAB=60�㣬
���BAC=30�㣬��AB=6��
��BM=2$\sqrt{3}$��
�ߡ�OBM=30�㣬BM=2$\sqrt{3}$��
��OM=$\sqrt{3}$��
���M��������$\sqrt{3}$��0����
���� �����Ǽ��α任�ۺ��⣬��Ҫ������Գƺ����·�����⣬�漰�����Σ������ε����ʣ��ȱ������ε����ʣ��Ȿ��Ĺؼ���ȷ�������·�ߵ�λ�ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�콭��ʡ�߰��о��꼶��ѧ�ڵ�һ��ģ�⿼����ѧ�Ծ��������棩 ���ͣ������
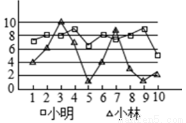
������ѧԱС�ֺ�С����ϰ�������һ��10ǹ��������˴�еĻ�����ͼ��ʾ��ͨ�����ֵijɼ���̫�ȶ�����ô����ͼ�е���Ϣ������С�ֺ�С��������������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ��ұ�о��꼶3���п�ģ����ѧ�Ծ��������棩 ���ͣ������
��ͼ������ABC�ı߳�Ϊ2����BC���ϵĸ�AB1Ϊ��������AB1C1����ABC���AB1C1�������ֵ������ΪS1����������AB1C1��B1C1�ϵĸ�AB2Ϊ��������AB2C2����AB1C1���AB2C2�������ֵ������ΪS2�������Դ����ƣ���ôS3 = ______,��Sn=______�����ú�n��ʽ�ӱ�ʾ��
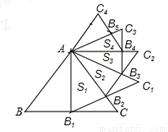
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ��ұ�о��꼶3���п�ģ����ѧ�Ծ��������棩 ���ͣ���ѡ��
ʵ����17���෴���ǣ�������
A. 17 B. 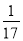 C. ��17 D. ��
C. ��17 D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
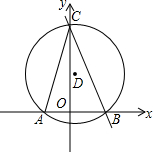 ��֪����ͼ����ƽ��ֱ������ϵ�У�A��-2��0����B��3��0����ֱ��l��y=kx+b����B�㣬��y��������ύ��C�㣬����AC����ʱ��ACB=45�㣬��һ��D������ABC���������㣮
��֪����ͼ����ƽ��ֱ������ϵ�У�A��-2��0����B��3��0����ֱ��l��y=kx+b����B�㣬��y��������ύ��C�㣬����AC����ʱ��ACB=45�㣬��һ��D������ABC���������㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
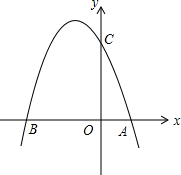 ��ͼ��������y=-x2-2x+3��y�ύ�ڵ�C����x�ύ�ڵ�A��B����B�ڵ�A����ࣩ����JΪy���������ϵ�һ���㣬����������y=-x2-2x+3����һ��K��ʹ�á�OKJΪ����ֱ�������Σ�
��ͼ��������y=-x2-2x+3��y�ύ�ڵ�C����x�ύ�ڵ�A��B����B�ڵ�A����ࣩ����JΪy���������ϵ�һ���㣬����������y=-x2-2x+3����һ��K��ʹ�á�OKJΪ����ֱ�������Σ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com