
 考前必练系列答案
考前必练系列答案科目:初中数学 来源:2017届江西省高安市九年级下学期第一次模拟考试数学试卷(解析版) 题型:单选题
为了调查瑞州市2016年初三年级学生的身高,从中抽取出200名学生进行调查,这个问题中样本容量为( )
A. 被抽取的200名学生的身高 B. 200 C. 200名 D. 初三年级学生的身高
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
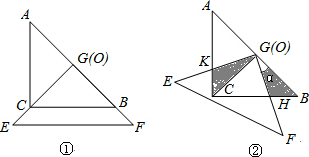
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
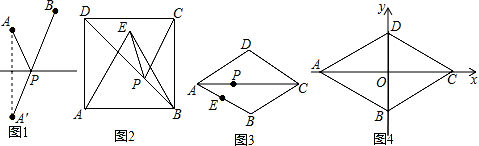
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
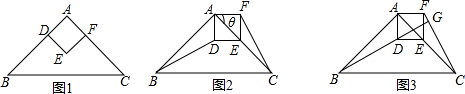
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
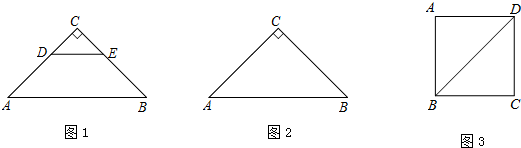
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
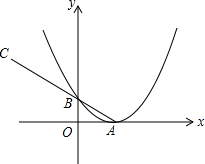 如图,抛物线y=$\frac{1}{4}$x2-x+1的顶点A在x轴上,与y轴交于B,延长AB至C,使BC=2AB,将抛物线向左平移n个单位,使抛物线与线段AC总有两个交点,求n的取值范围.
如图,抛物线y=$\frac{1}{4}$x2-x+1的顶点A在x轴上,与y轴交于B,延长AB至C,使BC=2AB,将抛物线向左平移n个单位,使抛物线与线段AC总有两个交点,求n的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com