
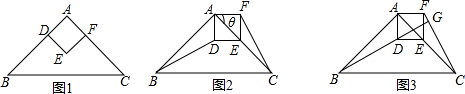
分析 (1)由△ABC是等腰直角三角形和ADEF是正方形得到判断△ABD≌△ACF的条件;
(2)由全等得到∠BGC=90°,利用勾股定理计算即可.
解答 解:(1)BD=CF成立.
理由:∵△ABC是等腰直角三角形,
∴AB=AC,
∵ADEF是正方形,
∴AD=AF,∠BAC=∠DAF,
∴∠BAC-∠DAC=∠DAF-∠DAC,
即∠BAD=∠CAF,
在△ABD和△ACF中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$
∴△ABD≌△ACF,
∴BD=CF.
(2)①由(1)全等得:∠ABD=∠ACE,
∴∠GBC+∠GCB=∠GBC+∠ACF+∠ACB=(∠ABG+∠GBC)+∠ACB=45°+45°=90°,
∴∠BGC=90°,
∴BG⊥CF.
②如图3,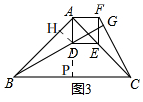
过D作DH⊥AB于H,AH=DH=AD÷$\sqrt{2}$=1,
∴BH=AB-AH=4,
∴BD=$\sqrt{B{H}^{2}+D{H}^{2}}$=$\sqrt{17}$,
延长AD交BC于P,
∴DP⊥BC,BP=$\frac{1}{2}$BC=$\frac{5\sqrt{2}}{2}$(AD平分∠BAC,AB=AC,等腰三角形三线合一)
由∠BGC=90°,
∴∠BPD=∠BGC,
∵∠DBP=∠CBG,
∴△DBP∽△CBG,
∴$\frac{BD}{BC}=\frac{BP}{BG}$,
∵BC=$\sqrt{2}$AB=5$\sqrt{2}$,
∴$\frac{\sqrt{17}}{5\sqrt{2}}=\frac{\frac{5\sqrt{2}}{2}}{BG}$
∴BG=$\frac{25\sqrt{17}}{17}$.
点评 此题是几何变换的综合题,主要考查等腰直角三角形和正方形的性质,平行线分线段成比例定理,判断出全等是解决本题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源:2016-2017学年浙江省杭州市萧山区戴村片八年级3月月考数学试卷(解析版) 题型:判断题
某汽车销售公司2月份销售某厂汽车,在一定范围内,每辆汽车的进价与销售量有如下关系:若当月仅售出1辆汽车,则该汽车的进价为30万元;每多售出1辆,所有售出汽车的进价每辆均降低0.1万元,月底厂家一次性返利给销售公司,每辆返利0.5万元.
(1)如果该公司当月售出7辆汽车,那么每辆汽车的进价为多少万元?
(2)如果汽车的售价为每辆31万元,该公司计划当月盈利12万元,那么需要售出多少辆汽车?(盈利=销售利润+返利)
查看答案和解析>>
科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:单选题
在初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
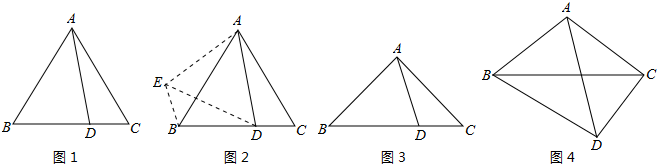
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
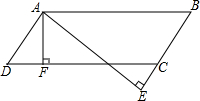 如图,过?ABCD的顶点A分别作AF⊥DC于F,AE⊥BC交BC的延长线于点E,若AE=3.5cm,AF=2.8cm,∠EAF=30°,则AB=7cm,AD=5.6cm.
如图,过?ABCD的顶点A分别作AF⊥DC于F,AE⊥BC交BC的延长线于点E,若AE=3.5cm,AF=2.8cm,∠EAF=30°,则AB=7cm,AD=5.6cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
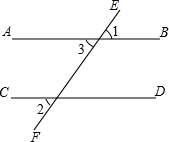 (1)如图,已知直线EF与AB、CD都相交,AB∥CD.
(1)如图,已知直线EF与AB、CD都相交,AB∥CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com