
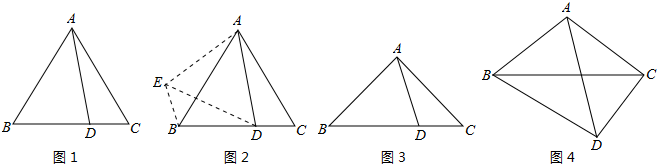
分析 (1)把△ACD绕点A顺时针旋转90°得到△ABE,连接ED,则易证△ACD≌△ABE,根据勾股定理可以的到DE=$\sqrt{2}$AD,在△DBE中利用两边之和大于第三边即可得到;
(2)把△ACD绕点A顺时针旋转90°得到△ABE,连接ED,则易证△ACD≌△ABE,△AED是等腰直角三角形,则DE=AD,在△BED中,利用三角形三边关系定理即可证得;
(3)把△ACD绕点A顺时针旋转α,得到△ABE,则有△ACD≌△ABE,则易证E、B、D三点共线,在等腰△ADE中,利用两边之和大于第三边即可得到.
解答 (1)证明:如图1,
把△ACD绕点A顺时针旋转90°得到△ABE,
则有△ACD≌△ABE,DC=EB
∵AD=AE,∠DAE=90°
∴△ADE是等腰直角三角形
∴DE=$\sqrt{2}$AD
在△DBE中,BD+EB>DE,
即:BD+DC>$\sqrt{2}$AD;
(2)如图2,
把△ABD旋转,使AB与AC重合,得到△ACD′,
则BD=CD′,
在△CDD′中,CD+CD′>DD′,
即:BD+CD>DD′,
∵△ADD′是钝角三角形,则DD′>$\sqrt{2}$AD,
当D运动到B的位置时,DD′=BC=AD.
∴BD+DC≥$\sqrt{2}$AD;
(3)猜想1:BD+DC<2AD
证明:如图3,
把△ACD绕点A顺时针旋转α,得到△ABE
则有△ACD≌△ABE,DC=EB,∠ACD=∠ABE
∵∠BAC+∠BDC=180°
∴∠ABD+∠ACD=180°
∴∠ABD+∠ABE=180°
即:E、B、D三点共线.
∵AD=AE,
∴在△ADE中,AE+AD>ED,
即BD+DC<2AD.
点评 此题是几何变换综合题,主要考查了旋转的性质以及勾股定理,通过旋转构造全等的三角形,把所研究的三条线段转移到同一个三角形中,是解题的关键.


科目:初中数学 来源:2017届江西省高安市九年级下学期第一次模拟考试数学试卷(解析版) 题型:填空题
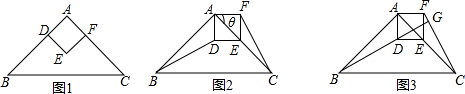
如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是___________。

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
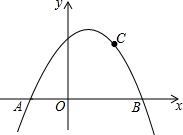 如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交于A,B两点,且AB=4,点C(2,$\frac{3}{2}$)在抛物线上.求抛物线的解析式.
如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交于A,B两点,且AB=4,点C(2,$\frac{3}{2}$)在抛物线上.求抛物线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
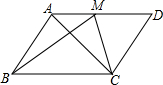 如图所示,?ABCD中,M为AD的中点,BM平分∠ABC,则( )
如图所示,?ABCD中,M为AD的中点,BM平分∠ABC,则( )| A. | CM可能垂直于AD | B. | AC不可能垂直于CD | ||
| C. | CM不可能垂直于AD | D. | CM可能平分∠ACD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
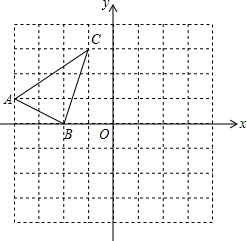 (1)请你把△ABC平移到△DEF,使点A(-4,1)的对应点D的坐标为(1,-2),B、C的对应点分别为E、F.
(1)请你把△ABC平移到△DEF,使点A(-4,1)的对应点D的坐标为(1,-2),B、C的对应点分别为E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com