
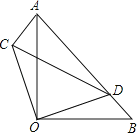
【题目】如图,△AOB,△COD是等腰直角三角形,点D在AB上.
(1)求证:△ACO≌△BDO;
(2)若∠BOD=30°,求∠ACD度数.
【答案】(1)证明见解析;(2)∠ACD=60°.
【解析】
(1)根据等腰直角三角形得出OC=OD,OA=OB,∠AOB=∠COD=90°,求出∠AOC=∠BOD,根据全等三角形的判定定理推出即可;
(2)根据全等三角形的性质求出∠BOD=∠ACO=30°,∠CAO=∠OBD=45°,然后利用三角形内角和求出∠ACO,进而求解.
解:(1)∵△AOB,△COD是等腰直角三角形,
∴OC=OD、AO=BO、∠COA+∠AOD=∠DOB+∠AOD=90°,
∴∠COA=∠DOB,
∴△ACO≌△BDO (SAS),
(2)解:∵△ACO≌△BDO,
∴∠BOD=∠ACO=30°,∠CAO=∠OBD=45°,
∴∠ACO=180°﹣30°﹣45°=105°,
∴∠ACD∠ACO﹣∠OCD=105°﹣45°=60°.


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
从上表可知,下列说法正确的有多少个
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是直线x=![]() ;
;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减少.
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
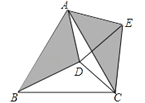
【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为 ( )
A. ![]() B. 2
B. 2![]() C. 3
C. 3![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为![]() 米的篱笆围成,若墙长为
米的篱笆围成,若墙长为![]() 米,设这个苗圃垂直于墙的一边长为
米,设这个苗圃垂直于墙的一边长为![]() 米.
米.

![]() 若苗圃园的面积为
若苗圃园的面积为![]() 平方米,求
平方米,求![]() 的值;
的值;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧![]() 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是

A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(﹣60°)=﹣![]() ;
;
②sin75°=![]() ;
;
③sin2x=2sinxcosx;
④sin(x﹣y)=sinxcosy﹣cosxsiny.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,把△ABC绕AB边上的点D顺时针旋转,旋转角为α(0°<α<180°),得到Rt△A′DE,A′C′交AB于点E,若AD=BE,则AD的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOBC的边OB、OA分别在x、y轴上,点C坐标为(8,8),将正方形AOBC绕点A逆时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段BC于点Q,ED的延长线交线段OB于点P,连接AP、AQ.
(1)求证:△ACQ≌△ADQ;
(2)求∠PAQ的度数,并判断线段OP、PQ、CQ之间的数量关系,并说明理由;
(3)连接BE、EC、CD、DB得到四边形BECD,在旋转过程中,四边形BECD能否是矩形?如果能,请求出点P的坐标,如果不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com