
【题目】如图,在△ABC中,AB=8, AC=10,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,连接GD,若∠EFC=60°,则EG的长为( )

A. 4B. 5C. 6D. 7
【答案】B
【解析】
连接BD取BD中点为H,连接HF、HE,利用中位线的性质及等腰三角形的性质,在△AFG中找到各角之间的关系,继而可得△AGF是等边三角形,推出GF、FE各自的边长,继而得到GE的长度.
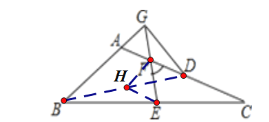
连接BD取BD中点H,连接HF、HE.
因为F是AD的中点,
所以HF∥AB,HF=![]() AB,
AB,
所以∠AGF=∠HFE,HF=4.
同理HE∥CD,HE=![]() CD,
CD,
所以∠HEF=∠EFC=60°.
又因为AB=CD=8,
所以HE=4.
因为∠HFE=60°,HE=HF=4,
所以△HEF为等边三角形,
所以EF=4.
因为∠AGE=∠AFG=60°,
所以△AGF为等边三角形.
因为F为AD中点且AD=2,
所以GF=1.
因为GE=EF+GF,
所以GE=5.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
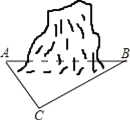
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,BE平分∠ABC交AC于点F,交AD于点E,且∠DBF=15°,求证:(1)AO=AE; (2)∠FEO的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
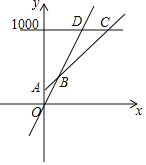
【题目】某游乐场普通门票价格40元/张,为了促销,新推出两种办卡方式:
①白金卡售价200元/张,每次凭卡另收取20元;
②钻石卡售价1000元/张,每次凭卡不再收费.
促销期间普通门票正常出售,两种优惠卡不限次数,设去游乐场玩x次时,所需总费用为y元.
(1)分别写出选择白金卡、普通门票消费时,y与x之间的函数关系式.
(2)在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点B,C的坐标.
(3)请根据图象,直接写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/s秒的速度从点A出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动,点P运动到F点时停止运动,点Q也同时停止运动,当点P运动__秒时,以P、Q、E、F为顶点的四边形是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
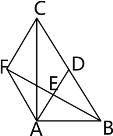
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1) 求证:AF=DC;
(2) 若AC⊥AB,试判断四边形ADCF的形状,并说明理由;
(3) 当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
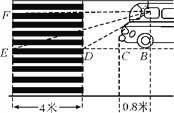
【题目】如图,某小学门口有一直线马路,交警在门口设有一条宽度为4米的斑马线,为安全起见,规定车头距斑马线后端的水平距离不得低于2米,现有一旅游车在路口遇红灯刹车停下,汽车里司机与斑马线前后两端的视角分别为∠FAE=15°和∠FAD=30°,司机距车头的水平距离为0.8米,试问该旅游车停车是否符合上述安全标准?(E,D,C,B四点在平行于斑马线的同一直线上)(参考数据:tan15°=2-![]() ,
,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
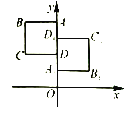
【题目】如图,正方形ABCD 与正方形![]() 关于某点中心对称.已知A,
关于某点中心对称.已知A,![]() ,D三点的坐标分别是(0,4),(0,3),(0,2).
,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标:
(2)写出顶点B,C,![]() 的坐标。
的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com