
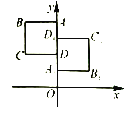
【题目】如图,正方形ABCD 与正方形![]() 关于某点中心对称.已知A,
关于某点中心对称.已知A,![]() ,D三点的坐标分别是(0,4),(0,3),(0,2).
,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标:
(2)写出顶点B,C,![]() 的坐标。
的坐标。
【答案】(1) (0,![]() );(2) B(-2,4)、B1(2,1)、C(-2,2)、C1(2,3)
);(2) B(-2,4)、B1(2,1)、C(-2,2)、C1(2,3)
【解析】试题分析:
(1)由题意可知点D、D1关于题中的对称中心对称,由此可得对称中心是线段DD1的中点,根据D、D1的坐标求得线段DD1的中点坐标即可;
(2)由所给A、D两点的坐标可求得正方形ABCD的边长,结合图形即可求得点B、C的坐标;由题意可知两个正方形的边长相等,这样结合图形和点D1的坐标即可求得B1、C1的坐标了.
试题解析:
(1)∵D和D1是对称点,
∴对称中心是线段DD1的中点.
∴对称中心的坐标是(0,![]() ).
).
(2)∵已知A,D两点的坐标分别是(0,4),(0,2),
∴正方形的边长为2.
∵A,B纵坐标相同,
∴B(-2,4)
∵C点纵坐标与D点纵坐标相同,横坐标与B点横坐标相同,
∴C(-2,2).
∵C1,D1纵坐标相同,正方形边长为2,
∴C1(2,3).
∵C1,B1横坐标相同,B1,A1纵坐标相同,
∴B1(2,1).


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8, AC=10,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,连接GD,若∠EFC=60°,则EG的长为( )

A. 4B. 5C. 6D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() .求
.求![]() 的度数.
的度数.

请将求![]() 的度数的过程及理由填写出来.
的度数的过程及理由填写出来.
解:∵![]() (已知),
(已知),
∴![]() (______________________).
(______________________).
又∵![]() (已知),
(已知),
∴![]() (______________________).
(______________________).
∴![]() __________(______________________).
__________(______________________).
∴![]() __________
__________![]() (______________________).
(______________________).
又∵![]() (已知),
(已知),
∴![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
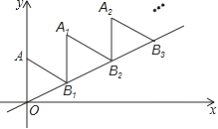
【题目】如图,放置的![]() ,
, ![]() ,
, ![]() ,…都是边长为2的等边三角形,边
,…都是边长为2的等边三角形,边![]() 在
在![]() 轴上,点
轴上,点![]() ,
, ![]() ,
, ![]() ,…都在直线
,…都在直线![]() 上,则
上,则![]() 的坐标是( )
的坐标是( )
A. (2017,2017![]() ) B. (2017
) B. (2017![]() ,2017)
,2017)
C. (2017,2018) D. (2017![]() ,2019)
,2019)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点P的坐标为(2a+6,a-3)
(1)当点P的纵坐标为-4,求a的值;
(2)若点P在y轴上,求点P的坐标;
(3)若点P在第四象限,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①
中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①![]() ;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若
;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若![]() ,则
,则![]() ;其中正确的有( )
;其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索:在图1至图2中,已知![]() 的面积为a
的面积为a

(1)如图1,延长![]() 的边BC到点D,使CD=BC,连接DA;延长边CA到点E,使CA=AE,连接DE;若
的边BC到点D,使CD=BC,连接DA;延长边CA到点E,使CA=AE,连接DE;若![]() 的面积为
的面积为![]() ,则
,则![]() = (用含a的代数式表示);
= (用含a的代数式表示);
(2)在图1的基础上延长AB到点F,使BF=AB,连接FD,FE,得到![]() (如图2).若阴影部分的面积为
(如图2).若阴影部分的面积为![]() ,则
,则![]() = (用a含的代数式表示);
= (用a含的代数式表示);
(3)发现:像上面那样,将![]() 各边均顺次延长一倍,连接所得端点,得到
各边均顺次延长一倍,连接所得端点,得到![]() (如图2),此时,我们称
(如图2),此时,我们称![]() 向外扩展了一次.可以发现,扩展n次后得到的三角形的面积是
向外扩展了一次.可以发现,扩展n次后得到的三角形的面积是![]() 面积的 倍(用含n的代数式表示);
面积的 倍(用含n的代数式表示);
(4)应用:某市准备在市民广场一块足够大的空地上栽种牡丹花卉,工程人员进行了如下的图案设计:首先在![]() 的空地上种紫色牡丹,然后将
的空地上种紫色牡丹,然后将![]() 向外扩展二次(如图3).在第一次扩展区域内种黄色牡丹,第二次扩展区域内种紫色牡丹,紫色牡丹花的种植成本为100元/平方米,黄色牡丹花的种植成本为95元/平方米.要使得种植费用不超过48700元,工程人员在设计时,三角形
向外扩展二次(如图3).在第一次扩展区域内种黄色牡丹,第二次扩展区域内种紫色牡丹,紫色牡丹花的种植成本为100元/平方米,黄色牡丹花的种植成本为95元/平方米.要使得种植费用不超过48700元,工程人员在设计时,三角形![]() 的面积至多为多少平方米?
的面积至多为多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() 于
于![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和![]() 的度数.对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
的度数.对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
解:∵![]() ,
,![]() 平分
平分![]() (______)
(______)
∴![]() ______
______![]() ______
______![]() ______.(角平分线的定义)
______.(角平分线的定义)
∵![]() (已知)
(已知)
∴![]() ______
______![]() ______
______![]() ______.(______)
______.(______)
∵![]() (______)
(______)
∴![]() (等式的性质)
(等式的性质)
![]() ______(等量代换)
______(等量代换)
![]() ______.
______.
∵![]() 于
于![]() (已知)
(已知)
∴![]() (______)
(______)
在直角三角形![]() 中,
中,
∵![]() (______)
(______)
∴![]() (等式的性质)
(等式的性质)
![]() ______(等量代换)
______(等量代换)
![]() ______.
______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com