已知直线y=-2x+b(b≠0)与x轴交于点A,与y轴交于点B,抛物线的解析式为y=x2-(b+10)x+c.
(1)若b=-5,c=4,求抛物线与x轴的交点坐标;
(2)若该抛物线过点B,且它的顶点P在直线y=-2x+b上,试确定这条抛物线的解析式;
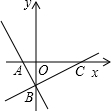
(3)过点B作直线BC⊥AB,交x轴于点C,若抛物线的对称轴恰好经过点C,求直线y=-2x+b的解析式.
解:(1)当b=-5,c=4时,抛物线的解析式为y=x
2-5x+4,
当y=0时,x
2-5x+4=0,
解得x
1=1,x
2=4,
所以,抛物线与x轴的交点坐标为(1,0)和(4,0);
(2)依题意得,A(

,0),B(0,b),
∵抛物线y=x
2-(b+10)x+c过点B,
∴b=c,
∴抛物线为y=x
2-(b+10)x+b,
又∵抛物线y=x
2-(b+10)x+b的顶点(
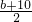
,
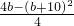
)在直线y=-2x+b上,
∴
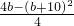
=-2•
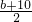
+b,
整理得,b
2+16b+60=0,
解得b
1=-10,b
2=-6,
所以,抛物线解析式为y=x
2-10或y=x
2-4x-6;
(3)如图所示,
若b>0,则点C在x轴负半轴,抛物线对称轴直线x=-
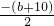
=
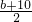
<0,
解得b<-10,无公共解,
若b<0,则点C在x轴正半轴,抛物线对称轴直线x=-
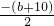
=
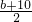
>0,
解得b>-10,有公共解;
所以,b<0,
则OA=-

,OB=-b,
又因为BC⊥AB,OB⊥AC,由射影定理得,
OB
2=OA•OC,
即(-b)
2=-

•OC,
解得OC=-2b,
∵抛物线的对称轴恰好经过点C,
∴-2b=
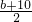
,
解得b=-2,
所以,直线解析式为y=-2x-2.
分析:(1)把b、c的值代入得到抛物线解析式,再令y=0,解关于x的一元二次方程即可得解;
(2)根据直线解析式求出点A、B的坐标,再根据抛物线过点B求出b=c,然后用b表示出抛物线顶点坐标,并代入直线解析式解方程求出b的值,从而得到抛物线解析式;
(3)先判定b<0,然后作出图形,根据射影定理求出OC,再根据抛物线的对称轴恰好过点C列式求出b的值,即可得解.
点评:本题是二次函数综合题型,主要考查了抛物线与x轴的交点坐标问题,抛物线的顶点坐标与对称轴解析式,求解较为复杂,但难度不大,(3)要注意先判断出b是负数.

 ,0),B(0,b),
,0),B(0,b),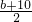 ,
,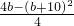 )在直线y=-2x+b上,
)在直线y=-2x+b上,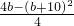 =-2•
=-2•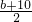 +b,
+b,
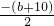 =
=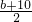 <0,
<0,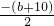 =
=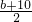 >0,
>0, ,OB=-b,
,OB=-b, •OC,
•OC,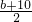 ,
,
