
����Ŀ����ͼ��������![]() ��x�ύA��B���㣨A����B����ࣩ��ֱ��
��x�ύA��B���㣨A����B����ࣩ��ֱ��![]() �������߽���A��C���㣬����C��ĺ�����Ϊ2��
�������߽���A��C���㣬����C��ĺ�����Ϊ2��
��1����A��B ��������꼰ֱ��AC�ĺ�������ʽ��
��2��P���߶�AC�ϵ�һ�����㣬��P����y���ƽ���߽���������E�㣬���߶�PE���ȵ����ֵ��
��3����G�������ϵĶ��㣬��x�����Ƿ���ڵ�F��ʹA��C��F��G�������ĸ���Ϊ������ı�����ƽ���ı��Σ�������ڣ������������������F�����ꣻ��������ڣ���˵�����ɣ�

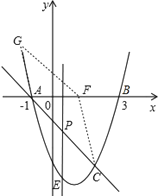
���𰸡�������
�������������������1����y=0����x2-2x-3=0���ɵ�AB�����ꣻ��C�ĺ�������룬���������꣬���A�����꣬�ɵ�BC�ķ��̣���2�����P��ĺ����꣬��ʾ��P��E�����꣬�ɵ�PE���ȵı���ʽ����������x��ȡֵ��Χ�ɵ��߶�PE���ȵ����ֵ������3����������һ����Ҫ��������۵ģ�������Է�Ϊ4�����������ʱ��������©����.
����������⣺��1����y=0�����![]() ��
��![]()
��A��-1��0��B��3��0����
��C������x=2����![]() ��y=-3����C��2��-3��
��y=-3����C��2��-3��
��ֱ��AC�ĺ�������ʽ��y="-x-1"
��2����P��ĺ�����Ϊx��-1��x��2��
��P��E������ֱ�Ϊ��P��x��-x-1����E��![]()
��P����E����Ϸ���PE=![]() ��2�֣�
��2�֣�
����![]() ʱ��PE�����ֵ=
ʱ��PE�����ֵ=![]()
��3������4�������ĵ�F���ֱ���![]()
����ͼ������C�������ߺ�y��Ľ��㣬��ôCG��x�ᣬ��ʱAF=CG=2�����F��������ǣ�-3��0����

����ͼ��AF=CG=2��A�������Ϊ��-1��0�������F�������Ϊ��1��0����
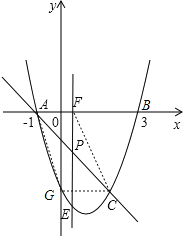
����ͼ����ʱC��G��������������x��Գƣ����G���������Ϊ3�������������м��ɵó�G�������Ϊ��1+![]() ��3��������ֱ��GF��б����ֱ��AC����ͬ����˿���ֱ��GF�Ľ���ʽΪy=-x+h����G������ɵó�ֱ�ߵĽ���ʽΪy=-x+4+
��3��������ֱ��GF��б����ֱ��AC����ͬ����˿���ֱ��GF�Ľ���ʽΪy=-x+h����G������ɵó�ֱ�ߵĽ���ʽΪy=-x+4+![]() �����ֱ��GF��x��Ľ���F������Ϊ��4+
�����ֱ��GF��x��Ľ���F������Ϊ��4+![]() ��0����
��0����
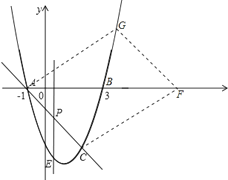
����ͼ��ͬ�������F������Ϊ��4-![]() ��0����
��0����
�ۺ���������ɵó�������4������������F�㣮


 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��֪�����ϵ�![]() ��
��![]() �ֱ��ʾ
�ֱ��ʾ![]() ��
��![]() ����
����![]() ��
��![]() ��Ϊ�෴����
��Ϊ�෴����![]() Ϊԭ��.
Ϊԭ��.
��1��![]() ______��
______��![]() ______��
______��
��2����������ij�����۵���ʹ�õ�![]() ���ʾ��10�ĵ��غϣ����ʱ���
���ʾ��10�ĵ��غϣ����ʱ���![]() �غϵĵ�����ʾ����Ϊ______��
�غϵĵ�����ʾ����Ϊ______��
��3������![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ��������
ͬʱ��������![]() ��ÿ��1����λ���ȵ��ٶ����������������˶�����
��ÿ��1����λ���ȵ��ٶ����������������˶�����![]() ��ÿ��2����λ���ȵ��ٶ����������������˶���
��ÿ��2����λ���ȵ��ٶ����������������˶���![]() ����
����![]() ������ԭ�ٷ��أ����˶�ʱ��Ϊ
������ԭ�ٷ��أ����˶�ʱ��Ϊ![]() ��.
��.
�ٵ�![]() ��ʾ������______���ú�
��ʾ������______���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��
����![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ��
��![]() ���3�������.
���3�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
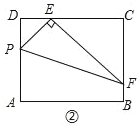
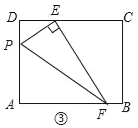
����Ŀ���ھ���ABCD�У�AD=3��CD=4����E��CD�ϣ���DE=1��
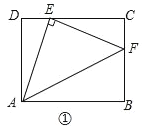
��1����֪����ͼ�٣�����AE������E��EF�AAE����BC�ڵ�F������AE����֤����ADE�ա�ECF������Ҫ֤������
��2��̽������ͼ�ڣ���P�ھ���ABCD�ı�AD�ϣ���P�����A��D�غϣ�������PE������E��EF��PE����BC�ڵ�F������PF����֤����PDE�͡�ECF���ƣ�
��3��Ӧ�ã���ͼ�ۣ���EF��AB�ڵ�F��EF�APE�������������䣬�ҡ�PEF�������6����AP�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ����
����![]() ��Ϊ��ǣ���
��Ϊ��ǣ���![]() ��Ϊ���ǣ�
��Ϊ���ǣ�![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��

��1����ͼ����![]() ʱ����
ʱ����![]() �Ķ�����
�Ķ�����
��2���ڣ�1���������£����㲹ȫͼ�Σ�����![]() �Ķ�����
�Ķ�����
��3����![]() ����
Ϊ����![]() ����ǣ���
����ǣ���![]() ��
��![]() ���غϲ���ʱ�������
���غϲ���ʱ�������![]() �Ķ���.��д��˵�����̣��ú�
�Ķ���.��д��˵�����̣��ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
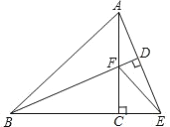
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ��ӳ�BC��EʹBE=BA������B��BD��AE�ڵ�D��BD��AC���ڵ�F������EF��
��1����֤��BF=2AD��
��2����CE=![]() ����AC�ij���
����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ܡ���ͬѧ����Ϥ��Ԣ�Թ��£���ͼ��ʾ����ʾ��Ԣ���еĹꡢ�õ�·��S��ʱ��t�Ĺ�ϵ������ֱ�߶α�ʾ�ڹ꣬���߶α�ʾ���ӣ�������������ȷ������ ��
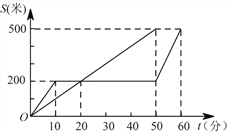
A. �����У����ӹ���Ϣ��50����
B. �ڹ�����α����е�ƽ���ٶ���0.1��/����
C. ���ӱ��ڹ��絽���յ�10����
D. �ڹ�����������20����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺(![]() )��2��
)��2��![]() +��
+��![]() ��4��0��
��4��0��![]() cos45�㣮
cos45�㣮
���𰸡�1
�������������������ԭʽ�ĵ�һ����ݸ�����ָ���ݵ����廯�ڶ����������ƽ�����Ķ������9������ƽ�����������������ָ����ʽ�������һ����������ǵ����Ǻ���ֵ���ϲ������ֵ.
���������ԭʽ=4��3+1��![]()
=2��1
=1��
�����͡������
��������
16
����Ŀ��������������������������һ�⣺�����ж���ͬ�������������ߣ������������Ҷ��У�������ʮ����б�������һᣮ�ʼ����и���������������˵����֪�ס��Ҷ���ͬʱ��ͬһ��
����������ٶ�Ϊ7���ҵ��ٶ�Ϊ3����һֱ���ߣ�����������10��������б��ƫ����������һ�κ�������������ô����ʱ�������Ҹ����˶�Զ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() Ϊ����
����
��1��![]() ��ȡ�� �����С����ֵ�� ����ʱ
��ȡ�� �����С����ֵ�� ����ʱ![]() = ��
= ��
��2��![]() +2��ȡ�� �����С����ֵ�� ����ʱ
+2��ȡ�� �����С����ֵ�� ����ʱ![]() = ��
= ��
��3��![]() ��ȡ�� �����С����ֵ�� ����ʱ
��ȡ�� �����С����ֵ�� ����ʱ![]() = ��
= ��
��4��![]() ��ȡ�� �����С����ֵ�� �� ��ʱ
��ȡ�� �����С����ֵ�� �� ��ʱ![]() = ��
= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����0ABC��ƽ��ֱ������ϵ�ڵ�λ����ͼ��ʾ����0Ϊ����ԭ�㣬��A������Ϊ(10��0)����B������Ϊ(10��8)����QΪ�߶�AC��-�㣬������Ϊ(5��n).
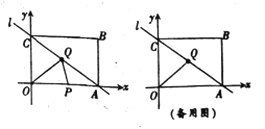
(1)��ֱ��AC�ı���ʽ
(2)��ͼ������PΪ��������-���㣬����P������AO��0C��·����ÿ��1����λ���ȵ��ٶ��˶�������C��ֹͣ����0PQ�����S���P���˶�ʱ��t(��)�ĺ�����ϵʽ.
(3)����PΪ����ƽ��������-.�㣬�Ƿ���������ĵ�P��ʹ��0��C��P��QΪ������ı���Ϊƽ���ı���?�����ڣ���ֱ��д����P�����꣬�������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com