
【题目】在矩形ABCD中,AD=3,CD=4,点E在CD上,且DE=1.
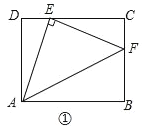
(1)感知:如图①,连接AE,过点E作EF丄AE,交BC于点F,连接AE,易证:△ADE≌△ECF(不需要证明);
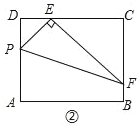
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE和△ECF相似;
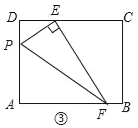
(3)应用:如图③,若EF交AB于点F,EF丄PE,其他条件不变,且△PEF的面积是6,则AP的长为_____.
【答案】3﹣![]()
【解析】试题分析:感知:先利用矩形性质得:∠D=∠C=90°,再利用同角的余角相等得:∠DAE=∠FEC,根据已知边的长度计算出AD=CE=3,则由ASA证得:△ADE≌△ECF;
探究:利用两角相等证明△PDE∽△ECF;
应用:作辅助线,构建如图②一样的相似三角形,利用探究得:△PDE∽△EGF,则 ![]() =
=![]() ,所以
,所以 ![]() =
=![]() ,再利用△PEF的面积是6,列式可得:PEEF=12,两式结合可求得PE的长,利用勾股定理求PD,从而得出AP的长.
,再利用△PEF的面积是6,列式可得:PEEF=12,两式结合可求得PE的长,利用勾股定理求PD,从而得出AP的长.
试题解析:证明:感知:如图①.∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠DAE+∠DEA=90°.∵EF⊥AE,∴∠AEF=90°,∴∠DEA+∠FEC=90°,∴∠DAE=∠FEC.∵DE=1,CD=4,∴CE=3.∵AD=3,∴AD=CE,∴△ADE≌△ECF(ASA);
探究:如图②.∵四边形ABCD为矩形,∴∠D=∠C=90°,∴∠DPE+∠DEP=90°.∵EF⊥PE,∴∠PEF=90°,∴∠DEP+∠FEC=90°,∴∠DPE=∠FEC,∴△PDE∽△ECF;
应用:如图③,过F作FG⊥DC于G.∵四边形ABCD为矩形,∴AB∥CD,∴FG=BC=3.∵PE⊥EF,∴S△PEF=![]() PEEF=6,∴PEEF=12,同理得:△PDE∽△EGF,∴
PEEF=6,∴PEEF=12,同理得:△PDE∽△EGF,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴EF=3PE,∴3PE2=12,∴PE=±2.∵PE>0,∴PE=2.在Rt△PDE中,由勾股定理得:PD=
,∴EF=3PE,∴3PE2=12,∴PE=±2.∵PE>0,∴PE=2.在Rt△PDE中,由勾股定理得:PD=![]() =
=![]() ,∴AP=AD﹣PD=3﹣
,∴AP=AD﹣PD=3﹣![]() .故答案为:3﹣
.故答案为:3﹣![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E、F在BD上,且BF=DE.
(1)写出图中所有你认为全等的三角形;
(2)延长AE交BC的延长线于G,延长CF交DA的延长线于H(请补全图形),证明四边形AGCH是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,反比例函数y=![]() (x>0),过点A(3,4).
(x>0),过点A(3,4).
(1)求y关于x的函数表达式.
(2)求当y≥2时,自变量x的取值范围.
(3)在x轴上有一点P(1,0),在反比例函数图象上有一个动点Q,以PQ为一边作一个正方形PQRS,当正方形PQRS有两个顶点在坐标轴上时,画出状态图并求出相应S点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点O出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,5秒后,两点相距15个单位长度,已知点B的速度是点A的速度的2倍(速度单位:单位长度/秒)
![]()
(1)求出点A、点B运动的速度;并在数轴上标出A、B两点从原点O出发运动5秒时的位置.
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,
①再过几秒,A、B两点重合?
②再过几秒,可以让A、B、O三点中一点是另外两点所成线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全解题过程.
已知:如图,O是直线AB上的一点,∠COD=90°,OE平分∠BOC.若∠AOC=60°,求∠DOE数.
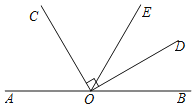
解:∵O是直线AB上的一点,(已知)
∴∠BOC=180°﹣∠AOC.(_________)
∵∠AOC=60°,(已知)
∴∠BOC=120°.(_________)
∵OE平分∠BOC,(已知)
∴∠COE=![]() ∠BOC,(_________)
∠BOC,(_________)
∴∠COE=_____°.
∵∠DOE=∠COD﹣∠COE,且∠COD=90°,
∴∠DOE=_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
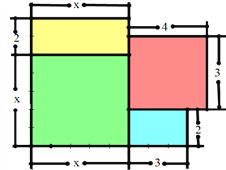
【题目】李叔叔在“中央山水”买了一套经济适用房,他准备将地面铺上地砖,这套住宅的建筑平面(由四个长方形组成)如图所示(图中长度单位:米),请解答下问题:
(1)用式子表示这所住宅的总面积;
(2)若铺1平方米地砖平均费用120元,求当x=6时,这套住宅铺地砖总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线![]() 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B 两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华间学早晨跑步,他从自己家出发.先向东跑了2km则达小盛家,又继续向东跑了1.5km到这小昌家,然后又向西跑到学校.如果小华跑步的速度是均匀的,且到达小盛家用了8分钟,整个跑步过程共用时32分钟,以小华家为原点,向东为正方向,用1个单位长度表示1km,建立数轴.
(1)依题意画出数轴,分别用点A表示出小盛家、用点B表示出小昌家;
(2)在数轴上,用点C表示出学校的位置;
(3)求小盛家与学校之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com