
| 4x |
| 3 |
科目:初中数学 来源:不详 题型:解答题
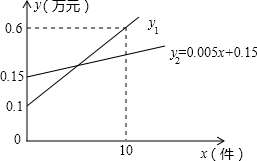
| 型号 | 甲 | 乙 | 丙 |
| 进价(万元/件) | 0.5 | 0.8 | 0.7 |
| 售价(万元/件) | 0.8 | 1.2 | 0.9 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 3 |
| 4 |
 两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
两点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=100t(15<t≤23) | B.y=100t-500(15<t≤23) |
| C.y=50t+650(15<t≤23) | D.y=100t+500(15<t≤23) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 已知油箱中的余油量y(升)与行驶时间t(小时)的关系如下表,
已知油箱中的余油量y(升)与行驶时间t(小时)的关系如下表,| 行驶时间t(时) | 0 | 1 | 2 | 3 |
| 油箱余油量y(升) | 100 | 84 | 68 | 52 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com