
 沿着折痕
沿着折痕 折叠,使点
折叠,使点 落在边
落在边 的中点
的中点 处,那么四边形
处,那么四边形 的面积等于 .
的面积等于 .


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
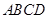 中,
中,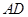 ∥
∥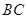 ,
,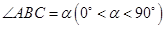 ,
,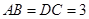 ,
,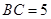 .点
.点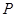 为射线
为射线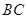 上动点(不与点
上动点(不与点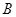 、
、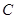 重合),点
重合),点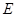 在直线
在直线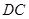 上,且
上,且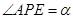 .记
.记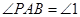 ,
,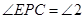 ,
,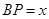 ,
,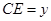 .
.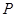 在线段
在线段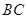 上时,写出并证明
上时,写出并证明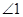 与
与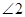 的数量关系;
的数量关系;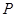 的运动,(1)中得到的关于
的运动,(1)中得到的关于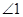 与
与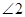 的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的
的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的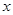 的取值范围;
的取值范围;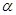 =
=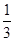 ,试用
,试用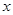 的代数式表示
的代数式表示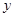 .
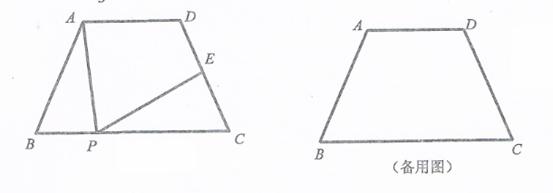
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
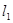 ∥
∥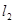 ,它们之间的距离等于a,一块正方形纸板
,它们之间的距离等于a,一块正方形纸板 的边长也等于a.现将这块硬纸板如图所示放在两条平行线上.
的边长也等于a.现将这块硬纸板如图所示放在两条平行线上.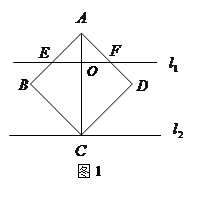
 上,且
上,且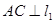 于O,使得直线
于O,使得直线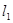 与
与 、
、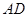 相交于E、F.求证:①BE="OE" ②
相交于E、F.求证:①BE="OE" ②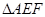 的周长等于
的周长等于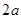 ;
;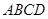 ,使得直线
,使得直线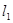 与
与 、
、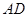 相交于E、F,试问
相交于E、F,试问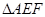 的周长等于
的周长等于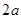 还成立吗?并证明你的结论;
还成立吗?并证明你的结论;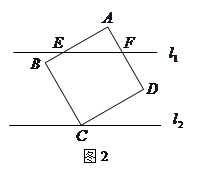
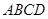 任意放置,使得直线
任意放置,使得直线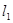 与
与 、
、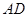 相交于E、F,直线
相交于E、F,直线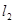 与
与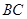 、CD相交于G,H,设
、CD相交于G,H,设 AEF的周长为
AEF的周长为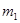 ,
, CGH的周长为
CGH的周长为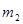 ,试问
,试问
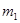 ,
,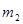 和
和 之间存在着什么关系?试直接写出你的结论(不需证明).
之间存在着什么关系?试直接写出你的结论(不需证明).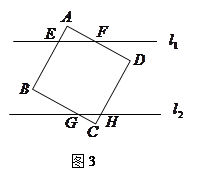
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
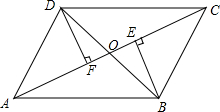
 BD,则四边形ABCD是什么特殊四边形?请说明理由.
BD,则四边形ABCD是什么特殊四边形?请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com