
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题:
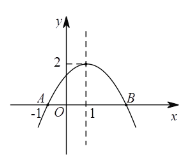
(1)点B的坐标为 ;
(2)y随x的增大而减小的自变量x的取值范围为 ;
(3)方程ax2+bx+c=0的两个根为 ;
(4)不等式ax2+bx+c<0的解集为 .
【答案】(1)(3,0);(2)x>1;(3)x1=-1,x2=3;(4)x<-1或x>3.
【解析】
(1)由图象可得:A、B到直线x=1的距离相等,根据A的坐标,即可求出B点坐标;
(2)利用图象得出函数对称轴进而得出y随x的增大而减小的自变量x的取值范围;
(3)根据方程ax2+bx+c=0,即图象与x轴交点,进而得出方程的两个根;
(4)利用不等式ax2+bx+c<0,即对应图象x轴下方的部分x的取值范围即可得出答案.
解:(1)由图象可得:A、B到直线x=1的距离相等,
∵A(-1,0)
∴B点坐标为:(3,0)
故答案为:(3,0);
(2)由图象可得:y随x的增大而减小的自变量x的取值范围是:x>1;
故答案为:x>1;
(3)∵方程ax2+bx+c=0,即图象与x轴交点,
∴方程ax2+bx+c=0的两个根是:x1=-1,x2=3;
故答案为:x1=-1,x2=3;
(4)由图象可得:不等式ax2+bx+c<0的解集是:x<-1或x>3;
故答案为:x<-1或x>3.


科目:初中数学 来源: 题型:
【题目】小军想用镜子测量一棵古松树的高度,但因树旁有一条小河,不能测量镜子与树之间的距离.于是他利用镜子进行两次测量.如图,第一次他把镜子放在点C处,人在点F处正好在镜中看到树尖A;第二次他把镜子放在点![]() 处,人在点F处正好在镜中看到树尖A.已知小军的眼睛距地面1.7m,量得
处,人在点F处正好在镜中看到树尖A.已知小军的眼睛距地面1.7m,量得![]() m,
m,![]() m,
m,![]() m.求这棵古松树的高度.
m.求这棵古松树的高度.
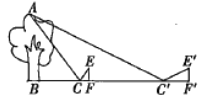
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个袋中均有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的数值分别为﹣7,﹣1,3,乙袋中的三张卡片上所标的数值分别为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用y表示取出的卡片上标的数值,把x、y分别作为点A的横坐标、纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况;
(2)求点A落在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:
x(天) | 1 | 2 | 3 | … |
m(kg) | 20 | 24 | 28 | … |
(1)请分别写出销售单价y(元/kg)与x(天)之间及销售量m(kg)是x(天)的之间的函数关系式.
(2)求在销售的第几天时,当天的利润最大,最大利润是多少?
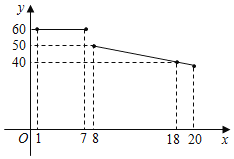
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,BC=2![]() .以BC的中点O为圆心的圆分别与AB,AC相切于D,E两点,则弧DE的长为( ).
.以BC的中点O为圆心的圆分别与AB,AC相切于D,E两点,则弧DE的长为( ).

A.![]() B.
B.![]() C.
C.![]() D.π
D.π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知动点P在边长为1的正方形ABCD的内部,点P到边AD、AB的距离分别为m、n.
(1)以A为原点,以边AB所在直线为x轴,建立平面直角坐标系,如图①所示,当点P在对角线AC上,且m=![]() 时,求点P的坐标;
时,求点P的坐标;
(2)如图②,当m、n满足什么条件时,点P在△DAB的内部?请说明理由.
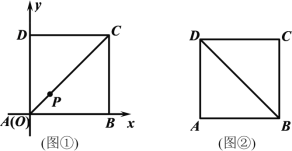
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点分别为A(1,2),B(2,5),C(6,1).若函数y=![]() 在第一象限内的图象与△ABC有交点,则k的取值范围是_____.
在第一象限内的图象与△ABC有交点,则k的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
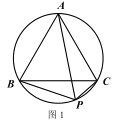
【题目】(1) 知识储备
①如图 1,已知点 P 为等边△ABC 外接圆的弧BC 上任意一点.求证:PB+PC= PA.
②定义:在△ABC 所在平面上存在一点 P,使它到三角形三顶点的距离之和最小,则称点 P 为△ABC
的费马点,此时 PA+PB+PC 的值为△ABC 的费马距离.
(2)知识迁移
①我们有如下探寻△ABC (其中∠A,∠B,∠C 均小于 120°)的费马点和费马距离的方法:
如图 2,在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆,根据(1)的结论,易知线段____的长度即为△ABC 的费马距离.
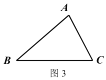
②在图 3 中,用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
(3)知识应用
①判断题(正确的打√,错误的打×):
ⅰ.任意三角形的费马点有且只有一个(__________);
ⅱ.任意三角形的费马点一定在三角形的内部(__________).
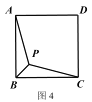
②已知正方形 ABCD,P 是正方形内部一点,且 PA+PB+PC 的最小值为![]() ,求正方形 ABCD 的
,求正方形 ABCD 的
边长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com