
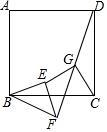
 已知:正方形ABCD和RT△BEF,BE=EF,G是DF中点,判断EG和CG的关系并说明理由.
已知:正方形ABCD和RT△BEF,BE=EF,G是DF中点,判断EG和CG的关系并说明理由. 分析 连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,由G为DF的中点,O为BD的中点,M为BF的中点,想办法证明△MEG≌△OGC,得到EG=CG,∠EGM=∠OCG,而∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,所以有∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°.
解答 解:结论:EG=CG且EG⊥CG.
理由:连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,如图,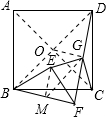
∵G为DF的中点,O为BD的中点,M为BF的中点,
∴OG∥BF,GM∥OB,
∴四边形OGMB为平行四边形,
∴OG=BM,GM=OB,
而EM=BM,OC=OB,
∴EM=OG,MG=OC,
∵∠DOG=∠GMF,
而∠DOC=∠EMF=90°,
∴∠EMG=∠GOC,
∴△MEG≌△OGC,
∴EG=CG,∠EGM=∠OCG,
又∵∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,
∴∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°,
∴EG=CG且EG⊥CG.
点评 本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角.也考查了三角形全等的判定与性质、三角形中位线的性质、直角三角形斜边上的中线性质以及正方形的性质.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$ | B. | $\sqrt{2}$-$\sqrt{3}$ | C. | $\sqrt{3}$-$\sqrt{2}$ | D. | -$\sqrt{2}$-$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
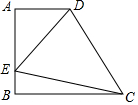 如图,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
如图,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知数轴上点A表示的数为8,B是数轴上原点左边的一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动.
如图,已知数轴上点A表示的数为8,B是数轴上原点左边的一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com